题目内容
【题目】设![]() ,
,![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() (
(![]() )的四个顶点,四边形
)的四个顶点,四边形![]() 是圆
是圆![]() :
:![]() 的外切平行四边形,其面积为
的外切平行四边形,其面积为![]() .椭圆
.椭圆![]() 的内接
的内接![]() 的重心(三条中线的交点)为坐标原点
的重心(三条中线的交点)为坐标原点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)![]() 的面积是否为定值?若是,求出该定值,若不是,请说明理由.
的面积是否为定值?若是,求出该定值,若不是,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)根据点到直线的距离以及菱形的面积公式可得到关于![]() 的二元二次方程组,解出方程组可得椭圆方程;(Ⅱ)当直线
的二元二次方程组,解出方程组可得椭圆方程;(Ⅱ)当直线![]() 斜率不存在时,易得三角形的面积,当直线
斜率不存在时,易得三角形的面积,当直线![]() 斜率存在时,设直线的方程
斜率存在时,设直线的方程![]() ,
, ![]() ,
, ![]() ,联立直线与椭圆的方程,运用韦达定理
,联立直线与椭圆的方程,运用韦达定理![]() 以及
以及![]() ,由
,由![]() 为重心,可得
为重心,可得![]() 点坐标,点
点坐标,点![]() 在椭圆上代入化简整理可得
在椭圆上代入化简整理可得![]() ,利用弦长公式以及点到直线的距离公式求出
,利用弦长公式以及点到直线的距离公式求出![]() 及
及![]() ,由
,由![]() 与整体代换思想相结合可得最后结果.
与整体代换思想相结合可得最后结果.
试题解析:(Ⅰ)因为四边形![]() 是圆
是圆![]() 外切平行四边形,所以
外切平行四边形,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,![]() ,
,
故所求椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)当直线![]() 斜率不存在时,因为
斜率不存在时,因为![]() 为
为![]() 的重心,故
的重心,故![]() 为左、右顶点,
为左、右顶点,
不妨设![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
易得![]() ,
,![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]() .
.
设直线![]() 方程为:
方程为:![]() ,
,![]() ,
,![]() .
.
由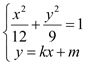 得
得![]() ,
,
则![]()
![]()
![]() .
.
即![]() ,
,
∴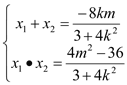 ,
,
∴![]() .
.
∵![]() 为
为![]() 的重心,∴
的重心,∴![]() ,
,
∵![]() 点在椭圆
点在椭圆![]() 上,故有
上,故有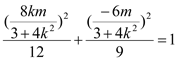 ,
,
化简得![]() .
.
∴![]()
![]() .
.
又点![]() 到直线
到直线![]() 的距离
的距离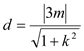 (
(![]() 是原点到
是原点到![]() 距离的3倍得到).
距离的3倍得到).
∴![]()
![]()
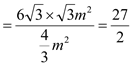 .
.
综上可得,![]() 的面积为定值
的面积为定值![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】某产品的广告费用x与销售额y的统计数据如下表
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程 ![]() =
= ![]() x+
x+ ![]() 的
的 ![]() 为9.4,据此模型预报广告费用为6万元时销售额为( )
为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元
B.65.5万元
C.67.7万元
D.72.0万元