题目内容
12.对于任意x∈R,令[x]为不大于x的最大整数,则函数f(x)=[x]称为高斯函数或取整函数.若数列{an}满足${a_n}=f(\frac{n}{4})$(n∈N+),且数列{an}的前n项和为Sn,则S4n等于2n2-n.分析 数列{an}满足${a_n}=f(\frac{n}{4})$=$[\frac{n}{4}]$,可得a4n-3=$[\frac{4n-3}{4}]$=$[n-1+\frac{1}{4}]$=n-1,同理可得a4n-2=n-1,a4n-1=n-1,a4n=n.即可得出S4n.
解答 解:∵数列{an}满足${a_n}=f(\frac{n}{4})$=$[\frac{n}{4}]$,
∴a4n-3=$[\frac{4n-3}{4}]$=$[n-1+\frac{1}{4}]$=n-1,
同理可得a4n-2=n-1,a4n-1=n-1,a4n=n.
∴S4n=(a1+a2+a3+a4)+(a4+1+a4+2+a4+3+a4+4)+…+(a4n-3+a4n-2+a4n-1+a4n)
=(0×3+1)+(1×3+2)+(2×3+3)+…+[(n-1)×3+n]
=$3×\frac{(n-1)×n}{2}$+$\frac{n(n+1)}{2}$
=2n2-n.
故答案为:2n2-n.
点评 本题考查了新定义高斯函数、等差数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
2.从装有5个红球和5个黑球的口袋中任取3个球,则至少有一个红球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{11}{12}$ |
20.(B题)设函数f(x)=$\frac{1-sinx}{x}$,x$∈(0,\frac{π}{2})$,则f(x)的单调性是( )
| A. | 增函数 | B. | 减函数 | C. | 先增后减函数 | D. | 先减后增函数 |
7.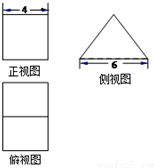 一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积是( )
一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积是( )
 一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积是( )
一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形,则该几何体的表面积是( )| A. | 64 | B. | 76 | C. | 88 | D. | 112 |
17.已知集合P={x|y=lg(2-x)},Q={x|x2-5x+4≤0},则P∩Q=( )
| A. | {x|1≤x<2} | B. | {x|1<x<2} | C. | {x|0<x<4} | D. | {x|0≤x≤4} |
4.已知△ABC中,a=$\sqrt{5}$,b=$\sqrt{15}$,∠A=30°,则c=( )
| A. | $\sqrt{15}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$或$\sqrt{5}$ | D. | $\sqrt{15}$或$\sqrt{5}$ |
5.某市为缓解春运期间的交通压力,计划在某路段实施“交通限行”,为了解公众对该路段“交通限行”的态度,某机构从经过该路段的人员随机抽查了50人进行调查,将调查情况进行整理,制成下表:
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在[65,75]的被调查者中随机选取2人进行进一步的采访,求选中的2人中恰好有1人赞成该路段“交通限行”的概率.

| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 9 | 6 | 4 | 3 |
(2)若从年龄在[65,75]的被调查者中随机选取2人进行进一步的采访,求选中的2人中恰好有1人赞成该路段“交通限行”的概率.
