题目内容
4．已知△ABC中，a=$\sqrt{5}$，b=$\sqrt{15}$，∠A=30°，则c=（ ）| A． | $\sqrt{15}$ | B． | $\sqrt{5}$ | C． | 2$\sqrt{5}$或$\sqrt{5}$ | D． | $\sqrt{15}$或$\sqrt{5}$ |
分析 利用已知及正弦定理可求sinB，进而可求B，C的值，再由正弦定理即可求c的值．
解答 解：∵a=$\sqrt{5}$，b=$\sqrt{15}$，∠A=30°，
∴由正弦定理可得：sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{15}×\frac{1}{2}}{\sqrt{5}}$=$\frac{\sqrt{3}}{2}$，
∴B=60°或120°．
∴C=180°-A-B=90°或30°，可得sinC=1或$\frac{1}{2}$
∴由c=$\frac{asinC}{sinA}$=可得c=2$\sqrt{5}$或$\sqrt{5}$．
故选：C．
点评 本题主要考查了正弦定理，三角形内角和定理的应用，解题时要注意讨论，不要漏解，属于基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
若函数f（x）=Asin（ωx+φ）的部分图象如图所示：
15．已知集合A={x|0＜x＜3}，B={x|-1＜x＜3}，则A∪B=（ ）
| A． | {x|-1＜x＜3} | B． | {x|0＜x＜3} | C． | {x|x＞-1} | D． | {x|x＜3} |
19．以（2，-1）为圆心且与直线3x-4y+5=0相交所得弦长为8的圆的标准方程为（ ）
| A． | （x-2）2+（y+1）2=9 | B． | （x+2）2+（y-1）2=9 | C． | （x-2）2+（y+1）2=25 | D． | （x+2）2+（y-1）2=25 |
16．已知P为△ABC所在平面内一点，且满足$\overrightarrow{AP}$=$\frac{1}{5}$$\overrightarrow{AC}$+$\frac{2}{5}$$\overrightarrow{AB}$，则△APB的面积与△APC的面积之比为（ ）
| A． | $\frac{1}{2}$ | B． | 2 | C． | $\frac{1}{3}$ | D． | 3 |
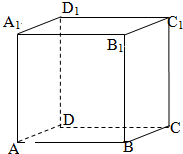ABCD-A1B1C1D1是单位正方体，黑白两只蚂蚁从点A出发沿棱向前爬行，每爬完一条棱称为“爬完一段”．白蚂蚁爬行的路线是AA1→A1D1，…，黑蚂蚁爬行的路线是AB→BB1，…，它们都遵循如下规则：所爬行的第i+2段与第i段所在直线必须是异面直线（i∈N*），设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处，则此时黑白蚂蚁的距离是（ ）