题目内容
【题目】已知抛物线C：y2=2px（p＞0）上的一点M的横坐标为3，焦点为F，且|MF|=4．直线l：y=2x﹣4与抛物线C交于A，B两点．
（Ⅰ）求抛物线C的方程；
（Ⅱ）若P是x轴上一点，且△PAB的面积等于9，求点P的坐标．
【答案】解：（Ⅰ）依题意得， 
+3=4，∴p=2，∴抛物线方程为C：y2=4x；
（Ⅱ）将直线方程与抛物线的方程进行联立，设A（x1 ， y1），B（x2 ， y2），
可得，y2﹣2y﹣8=0，∴A（1，﹣2），B（4，4），
∴|AB|= 
=3 
，
设P（a，0），P到直线AB的距离为d，则d=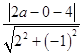 
= 
，
又S△ABP= 
|AB|d，
代入计算可得，|a﹣2|=3，
∴a=5或a=﹣1，
故点P的坐标为（5，0）和（﹣1，0）
【解析】（Ⅰ）代入计算即可得出答案；（Ⅱ）先求出AB的长度，再根据三角形的面积公式，即可求得点P的坐标．
练习册系列答案
相关题目
