题目内容
【题目】(12分)已知函数![]() .
.
(1)若x=2是函数f(x)的极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)在![]() 上为单调增函数,求a的取值范围;
上为单调增函数,求a的取值范围;
(3)设m,n为正实数,且m>n,求证: ![]() .
.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)导函数为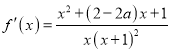 ,由
,由![]() ,解得并检验
,解得并检验![]() ,再求得
,再求得![]() ,切点为(1,0),由点斜式可求得切线方程。(2)由题意可
,切点为(1,0),由点斜式可求得切线方程。(2)由题意可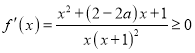 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上恒成立,分离参数得
上恒成立,分离参数得![]() ,所以
,所以![]() ,
, ![]()
![]() 。(3)由于是多个变量,所以利用变形,换元变成一个变量,变形为
。(3)由于是多个变量,所以利用变形,换元变成一个变量,变形为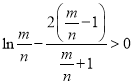 ,设
,设![]() .求导可证h(x)>0.
.求导可证h(x)>0.
试题解析:(1)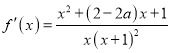 ,由题意知
,由题意知![]() ,代入得
,代入得![]() ,经检验,符合题意. 从而切线斜率
,经检验,符合题意. 从而切线斜率![]() ,切点为(1,0),所以切线方程为
,切点为(1,0),所以切线方程为![]()
(2)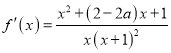 ,因为f(x)在
,因为f(x)在![]() 上为单调增函数,
上为单调增函数,
所以![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立.
上恒成立.
当![]() 时,由
时,由![]() ,得
,得![]() .
.
设![]()
![]()
![]() 。,
。, ![]() .
.
所以当且仅当![]() ,即x=1时,g(x)有最小值2.
,即x=1时,g(x)有最小值2.
所以![]() ,所以
,所以![]() .
.
所以a的取值范围是![]() .
.
(3)要证![]() ,只需证
,只需证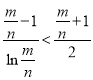 ,只需证
,只需证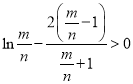 ,设
,设![]() .
.
由(2)知![]() 在
在![]() 上是单调增函数,又
上是单调增函数,又![]() .
.
所以![]() ,
,
即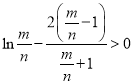 成立,所以
成立,所以![]()

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】某校高一年级共有1000名学生,其中男生400名,女生600名,该校组织了一次口语模拟考试(满分为100分).为研究这次口语考试成绩为高分(80分以上(含80分)为高分)是否与性别有关,现按性别采用分层抽样的方法抽取100名学生的成绩,按从低到高分成![]() 七组,并绘制成如图所示的频率分布直方图.已知区间
七组,并绘制成如图所示的频率分布直方图.已知区间![]() 上的频率等于区间
上的频率等于区间![]() 上频率,区间
上频率,区间![]() 上的频率与区间
上的频率与区间![]() 上的频率之比为
上的频率之比为![]() .
.
| 0.010 | 0.050 | 0.025 | 0.010 | 0.001 |
| 6.635 | 3.841 | 5.024 | 6.635 | 10.828 |
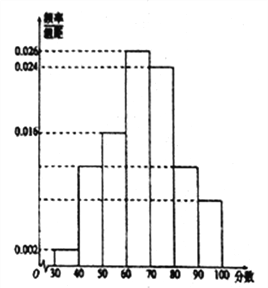
(1)估计该校高一年级学生在口语考试中,成绩为高分的人数;
(2)请你根据已知条件将下列![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“该校高一年级学生在本次考试中口语成绩及格(60分以上(含60分)为及格)与性别有关”.
的把握认为“该校高一年级学生在本次考试中口语成绩及格(60分以上(含60分)为及格)与性别有关”.
 附:
附: