题目内容

【题目】已知椭圆 + =1（a＞b＞0）的右焦点为F2（1，0），点H（2， ）在椭圆上．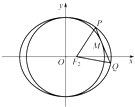
（1）求椭圆的方程；
（2）点M在圆x2+y2=b2上，且M在第一象限，过M作圆x2+y2=b2的切线交椭圆于P，Q两点，问：△PF2Q的周长是否为定值？如果是，求出定值；如果不是，说明理由．

【答案】
（1）解：∵椭圆 + =1（a＞b＞0）的右焦点为F2（1，0），点H（2， ）在椭圆上，

∴由题意，得 ，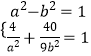

解得a=3，b=2

∴椭圆方程为


（2）解：设P（x1，y1），Q（x2，y2）， （|x1|≤3）

∴|PF2|2=（x1﹣1）2+y12= （x1﹣9）2，

∴|PF2|=3﹣ x1，

连接OM，OP，由相切条件知：

|PM|2=|OP|2﹣|OM|2=x12+y12﹣8=vx12，

∴|PM|= x1，

∴|PF2|+|PM|=3

同理可求|QF2|+|QM|=3

∴|F2P|+|F2Q|+|PQ|=6为定值


【解析】（1）由椭圆 + =1（a＞b＞0）的右焦点为F2（1，0），点H（2， ）在椭圆上，建立方程组，可得a值，进而求出b值后，可得椭圆方程；（2）设P（x1 ， y1），Q（x2 ， y2），分别求出|F2P|，|F2Q|，结合相切的条件可得|PM|2=|OP|2﹣|OM|2求出|PQ|，可得结论．

练习册系列答案
相关题目

【题目】已知抛物线C：y2=2px（p＞0）上的一点M的横坐标为3，焦点为F，且|MF|=4．直线l：y=2x﹣4与抛物线C交于A，B两点．
（Ⅰ）求抛物线C的方程；
（Ⅱ）若P是x轴上一点，且△PAB的面积等于9，求点P的坐标．

【题目】已知函数f（x）=lg（2+x）+lg（2﹣x）．

（1）求函数f（x）的定义域并判断函数f（x）的奇偶性；

（2）记函数g（x）= +3x，求函数g（x）的值域；

（3）若不等式 f（x）＞m有解，求实数m的取值范围．

【题目】如图，在Rt△ABC中，∠ACB＝，AC＝3， BC＝2，P是△ABC内的一点．

（1）若P是等腰直角三角形PBC的直角顶点，求PA的长；

（2）若∠BPC＝，设∠PCB＝θ，求△PBC的面积S(θ)的解析式，并求S(θ)的最大值．

【题目】设定义域为R的奇函数 （a为实数）． （Ⅰ）求a的值；
（Ⅱ）判断f（x）的单调性（不必证明），并求出f（x）的值域；
（Ⅲ）若对任意的x∈[1，4]，不等式f（k﹣ ）+f（2﹣x）＞0恒成立，求实数k的取值范围．

【题目】已知函数f（x）=x﹣ ．
（1）用函数单调性的定义证明：函数f（x）在区间（0，+∞）上为增函数；
（2）方程2tf（4t）﹣mf（2t）=0，当t∈[1，2]时，求实数m的取值范围．

【题目】已知数列的前项和为， ， ．等 差数列中， ，且公差．

（Ⅰ）求数列的通项公式；

（Ⅱ）是否存在正整数，使得?．若存在，求出的最小值；若 不存在，请说明理由．

【题目】已知函数y=f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x﹣x2 ．
（1）求x＜0时f（x）的解析式；
（2）问是否存在正数a，b，当x∈[a，b]时，g（x）=f（x），且g（x）的值域为[ ， ]？若存在，求出所有的a，b的值，若不存在，请说明理由．

【题目】已知函数f（x）=2x﹣2﹣x ， 若对任意的x∈[1，3]，不等式f（x2+tx）+f（4﹣x）＞0恒成立，则实数t的取值范围是 ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网