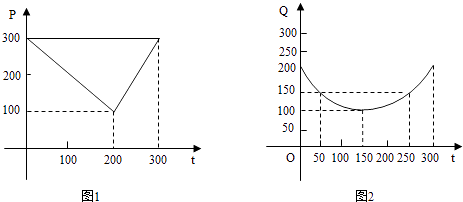��Ŀ����
����Ŀ�����г����飬ij��Ʒÿ�ֵļ۸�Ϊx��2��x��14��Ԫʱ������Ʒ���¹�����Ϊy1�֣�y1=ax��16��a��8������������Ϊy2��![]() ��������Ʒ����������С�ڹ�����ʱ�����������ڹ�������������Ʒ��������С�ڹ�����ʱ������������������������Ʒ�������۶�f��x����������������۸�ij˻���
��������Ʒ����������С�ڹ�����ʱ�����������ڹ�������������Ʒ��������С�ڹ�����ʱ������������������������Ʒ�������۶�f��x����������������۸�ij˻���
��1����a=32������Ʒ�ļ۸�Ϊ����Ԫʱ������Ʒ�������۶�f��x�����
��2�����������빩�������ʱ�ļ۸�Ϊ����۸�������Ʒ�ľ���۸���ÿ��10Ԫ����ʵ��a��ȡֵ��Χ��
���𰸡���1��![]() ��2��
��2��![]() .
.
�������������������1����������Ľ���ʽ��ͨ������x�ķ�Χ�Լ������ĵ�����������������ֵ���ɣ�
��2�����ݺ����ĵ����Ե�������a�IJ���ʽ�飬������ɣ�
���������
��1����a=32����y2��y1���é�x2��2x+224��32x��16�� ��é�40��x��6
��Ϊ2��x��14������2��x��6�������Ʒ�������۶�Ϊf��x����
��![]()
�ٵ�2��x��6ʱ��f��x��=��32x��16��x��
����f��x��max=f��6��=1056��Ԫ����
�ڵ�6��x��14ʱ��f��x��=����x2��2x+224��x��
��f'��x��=��3x2��4x+224=����x��8����3x+28����
��f'��x����0����x��8����f�䣨x����0����ã�x��8��
����f��x���ڣ�6��8���������������ڣ�8��14�����Ǽ�������
��x=8ʱ��f��x��max=f��8��=1152��Ԫ������
��Ϊ1152��1056������f��x��max=f��8��=1152Ԫ��
��2����![]() ��
��
��Ϊa��8������g��x�������䣨2��14��������������
������Ʒ�ľ���۸���10Ԫ��
������f��x��������[10��14��������㣬
����![]() ���
���![]() ��
��
����Ϊa��8������8��a��12��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�