题目内容
点A(0,2)是圆x2+y2=16内的定点,点B,C是这个圆上的两个动点,若BA⊥CA,求BC中点M的轨迹方程,并说明它的轨迹是什么曲线。
所求轨迹为以(0,1)为圆心,以 为半径的圆
为半径的圆
 为半径的圆
为半径的圆设点M(x,y),因为M是定弦BC的中点,故OM⊥BC, 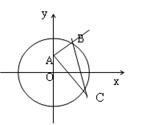
 又∵∠BAC=900 ,∴
又∵∠BAC=900 ,∴
∵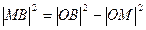 ,∴
,∴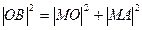
即: 42=(x2+y2)+[(x-0)2+(y-0)2]
化简为x2+y2-2y-6=0,即x2+(y-1)2="7."
∴所求轨迹为以(0,1)为圆心,以 为半径的圆。
为半径的圆。

 又∵∠BAC=900 ,∴
又∵∠BAC=900 ,∴
∵
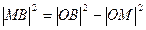 ,∴
,∴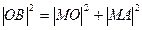
即: 42=(x2+y2)+[(x-0)2+(y-0)2]
化简为x2+y2-2y-6=0,即x2+(y-1)2="7."
∴所求轨迹为以(0,1)为圆心,以
 为半径的圆。
为半径的圆。
练习册系列答案
相关题目
 的直径
的直径 的延长线与弦
的延长线与弦 的延长线相交于点
的延长线相交于点 ,
, 为⊙
为⊙ 交
交 ,且
,且 ,
, 的长度.
的长度.
 关于直线
关于直线 对称的圆的方程.
对称的圆的方程.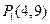 ,
,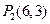 ,求以
,求以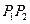 为直径的圆的方程,并判断
为直径的圆的方程,并判断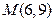 、
、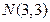 、
、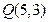 与圆的位置关系.
与圆的位置关系.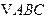 中,若两点
中,若两点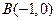 、
、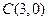 ,
,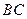 边中线
边中线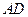 的长度为4,则点A的轨迹方程为( )
的长度为4,则点A的轨迹方程为( )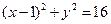
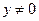 )
)
 )
)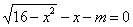 有实数解,则实数m的取值范围为( )
有实数解,则实数m的取值范围为( ) 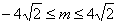
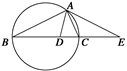
 于点A,割线
于点A,割线