题目内容
如图所示，设△ABC的外接圆的切线AE与BC的延长线交于点E，∠BAC的平分线与BC交于点D.求证：ED2=EC·EB.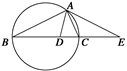
证明略
证明 如图所示，因为AE是圆的切线，
所以∠ABC=∠CAE.
又因为AD是∠BAC的平分线，所以∠BAD=∠CAD.
从而∠ABC+∠BAD=∠CAE+∠CAD.
因为∠ADE=∠ABC+∠BAD，
∠DAE=∠CAE+∠CAD，
所以∠ADE=∠DAE，故EA=ED.
因为EA是圆的切线，所以由切割线定理知，
EA2=EC·EB，
而EA=ED，所以ED2=EC·EB.
所以∠ABC=∠CAE.
又因为AD是∠BAC的平分线，所以∠BAD=∠CAD.
从而∠ABC+∠BAD=∠CAE+∠CAD.
因为∠ADE=∠ABC+∠BAD，
∠DAE=∠CAE+∠CAD，
所以∠ADE=∠DAE，故EA=ED.
因为EA是圆的切线，所以由切割线定理知，
EA2=EC·EB，
而EA=ED，所以ED2=EC·EB.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
，
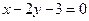
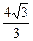
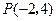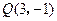，且在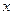
轴上截得的弦长为
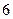的圆的方程．
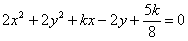表示的曲线为圆,则k的取值范围是( ) 
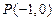的直线与圆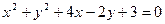
相切，则此直线在
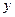轴上的截距是 __________________.