题目内容
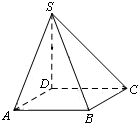
如图，四棱锥P-ABCD，PA⊥底面ABCD，AB∥CD，AB⊥AD，AB=AD=
CD=2，PA=2，M，E，F分别是PA，PC，PD的中点．
（1）证明：EF∥平面PAB；
（2）证明：PD⊥平面ABEF；
（3）求直线ME与平面ABEF所成角的正弦值．
| 1 |
| 2 |
（1）证明：EF∥平面PAB；
（2）证明：PD⊥平面ABEF；
（3）求直线ME与平面ABEF所成角的正弦值．
（1）证明：∵E、F分别是PC、PD的中点，∴EF∥CD，
∵AB∥CD，
∴AB∥EF，
∵EF?平面PAB，AB?平面PAB，
∴EF∥平面PAB；
（2）证明：∵PA⊥底面ABCD，AB?底面ABCD，
∴PA⊥AB，
∵AB⊥AD，PA∩AD=A，
∴AB⊥平面PAD，
∵AB∥EF，
∴EF⊥平面PAD，
∴EF⊥PD，
∵PA=AD=2，F是PD的中点，
∴PD⊥AF，
∵EF∩AF=F，
∴PD⊥平面ABEF；
（3）由（2）知，P到平面ABEF的距离为
，∴M到平面ABEF的距离为
，
又MF=1，EF=2，∴ME=
，
∴直线ME与平面ABEF所成角的正弦值为
=
．
∵AB∥CD，
∴AB∥EF，
∵EF?平面PAB，AB?平面PAB，
∴EF∥平面PAB；
（2）证明：∵PA⊥底面ABCD，AB?底面ABCD，
∴PA⊥AB，
∵AB⊥AD，PA∩AD=A，
∴AB⊥平面PAD，
∵AB∥EF，
∴EF⊥平面PAD，
∴EF⊥PD，
∵PA=AD=2，F是PD的中点，
∴PD⊥AF，
∵EF∩AF=F，
∴PD⊥平面ABEF；
（3）由（2）知，P到平面ABEF的距离为
| 2 |
| ||
| 2 |
又MF=1，EF=2，∴ME=
| 5 |
∴直线ME与平面ABEF所成角的正弦值为
| ||||
|
| ||
| 10 |
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
