题目内容
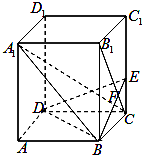
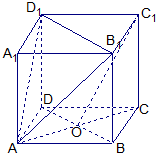
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.求证:
(1)C1O∥面A1B1D1;
(2)A1C⊥面AB1D1;
(3)求直线AC与平面AB1D1所成角的正切值.
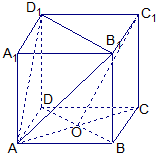
(1)C1O∥面A1B1D1;
(2)A1C⊥面AB1D1;
(3)求直线AC与平面AB1D1所成角的正切值.

证明:(1)连接A1C1,设A1C1∩B1D1=O1,
连接AO1,∵ABCD-A1B1C1D是正方体
∴A1ACC1是平行四边形
∴A1C1∥AC且A1C1=AC(2分)
又∵O1,O分别是A1C1,AC的中点,
∴O1C1∥AO且O1C1=AO
∴O1C1OA是平行四边形
∴C1O∥AO1,AO1?平面A1B1D1,C1O?平面A1B1D1,
∴C1O∥面A1B1D1;
(2)∵CC1⊥平面A1B1C1D1,
∴CC1⊥B1D1,
又∵A1C1⊥B1D1,
∴B1D1⊥平面A1C1C
即B1D1⊥A1C,
同理可证AB1⊥A1C,
又B1D1∩AB1=B1,
∴A1C⊥面AB1D1;
(3)直线AC与平面AB1D1所成的角实际上
就是正四面体ACB1D1的一条棱与一个面所成的角,
余弦值为
,从而正切值为
.(13分)
连接AO1,∵ABCD-A1B1C1D是正方体
∴A1ACC1是平行四边形
∴A1C1∥AC且A1C1=AC(2分)
又∵O1,O分别是A1C1,AC的中点,
∴O1C1∥AO且O1C1=AO
∴O1C1OA是平行四边形
∴C1O∥AO1,AO1?平面A1B1D1,C1O?平面A1B1D1,
∴C1O∥面A1B1D1;

(2)∵CC1⊥平面A1B1C1D1,
∴CC1⊥B1D1,
又∵A1C1⊥B1D1,
∴B1D1⊥平面A1C1C
即B1D1⊥A1C,
同理可证AB1⊥A1C,
又B1D1∩AB1=B1,
∴A1C⊥面AB1D1;
(3)直线AC与平面AB1D1所成的角实际上
就是正四面体ACB1D1的一条棱与一个面所成的角,
余弦值为
| ||
| 3 |
| 2 |

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目