题目内容
(本题满分12分)已知函数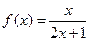 ,数列
,数列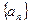 满足
满足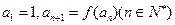 .
.
(Ⅰ)求证:数列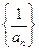 是等差数列;(Ⅱ)记
是等差数列;(Ⅱ)记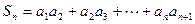 ,试比较
,试比较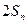 与1的大小.
与1的大小.
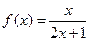 ,数列
,数列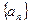 满足
满足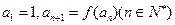 .
.(Ⅰ)求证:数列
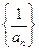 是等差数列;(Ⅱ)记
是等差数列;(Ⅱ)记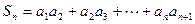 ,试比较
,试比较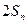 与1的大小.
与1的大小. (Ⅰ) 略 (Ⅱ) 

:(Ⅰ)由已知得,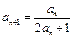 , ∴
, ∴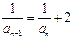 ,即
,即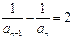 .
.
∴数列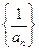 是首项
是首项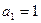 ,公差
,公差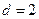 的等差数列.
的等差数列.
(Ⅱ) 由(Ⅰ)知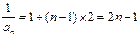 , ∴
, ∴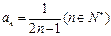 ,
,
∴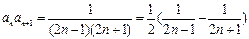 ,
,
∴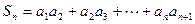
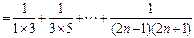
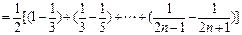
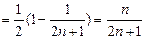 .
.
∴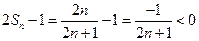
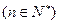 , ∴
, ∴ .
.
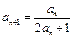 , ∴
, ∴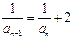 ,即
,即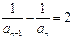 .
.∴数列
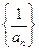 是首项
是首项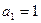 ,公差
,公差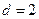 的等差数列.
的等差数列. (Ⅱ) 由(Ⅰ)知
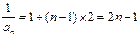 , ∴
, ∴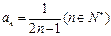 ,
,∴
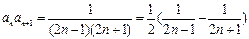 ,
,∴
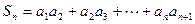
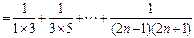
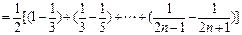
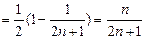 .
. ∴
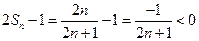
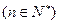 , ∴
, ∴ .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
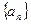 的前n项和为
的前n项和为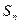 ,且对一切正整数n都有
,且对一切正整数n都有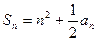 。
。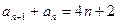 ;(2)求数列
;(2)求数列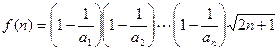 ,
,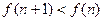 对一切
对一切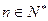 都成立。
都成立。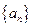 中,
中,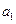 ,
,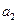 是给定的非零整数,
是给定的非零整数,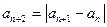 .
.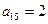 ,
,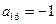 ,求
,求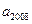 ;(2)证明:从
;(2)证明:从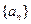 是公比大于1的等比数列,
是公比大于1的等比数列,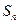 为数列
为数列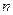 项和.已知
项和.已知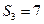 ,且
,且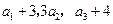 构成等差数列.
构成等差数列.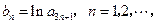 求数列
求数列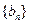 的前
的前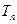 .
.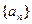 的通项公式为
的通项公式为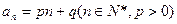 。数列
。数列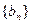 定义如下:对于正整数m,
定义如下:对于正整数m,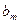 是使得不等式
是使得不等式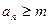 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若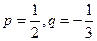 ,求b3; (2)若
,求b3; (2)若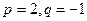 ,求数列
,求数列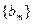 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得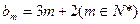 ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。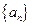 的前
的前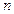 项和为
项和为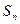 ,且满足
,且满足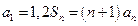 ;
;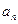 与
与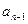 的关系式,并求
的关系式,并求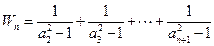 ;
;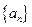 的前
的前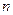 项和为
项和为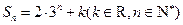
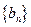 满足
满足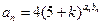 ,
, 为数列
为数列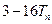 与
与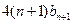 的大小,并证明你的结论.
的大小,并证明你的结论.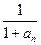 ,求a2008。
,求a2008。 的前n项和为Sn,已知S1,2S2,3S3成等差数列,则
的前n项和为Sn,已知S1,2S2,3S3成等差数列,则