题目内容
(本小题满分14分)
已知等比数列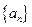 的前
的前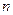 项和为
项和为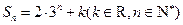
(Ⅰ)求数列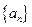 的通项公式;
的通项公式;
(Ⅱ)设数列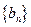 满足
满足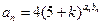 ,
, 为数列
为数列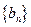 的前
的前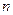 项和,试比较
项和,试比较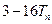 与
与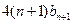 的大小,并证明你的结论.
的大小,并证明你的结论.
已知等比数列
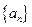 的前
的前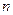 项和为
项和为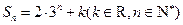
(Ⅰ)求数列
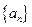 的通项公式;
的通项公式;(Ⅱ)设数列
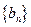 满足
满足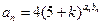 ,
, 为数列
为数列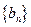 的前
的前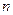 项和,试比较
项和,试比较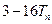 与
与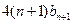 的大小,并证明你的结论.
的大小,并证明你的结论.(I)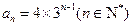 (II)当
(II)当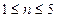
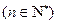 时有
时有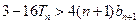
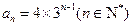 (II)当
(II)当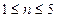
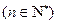 时有
时有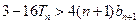
(Ⅰ)由 得:
得: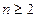 时,
时,
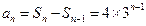 ………………………2分
………………………2分
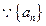 是等比数列,
是等比数列,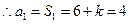
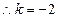 ,
,
得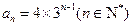 ……4分
……4分
(Ⅱ)由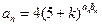 和
和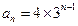 得
得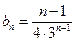 ……………………6分
……………………6分
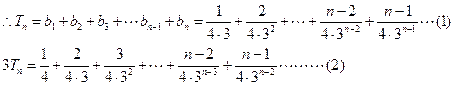
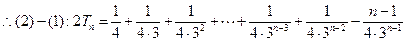
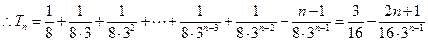 ……10分
……10分
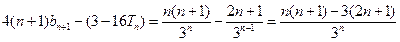
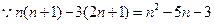 ………………………11分
………………………11分
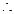 当
当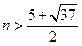 或
或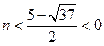 时有
时有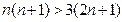 ,
,
所以当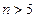
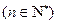 时有
时有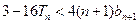
那么同理可得:当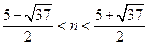 时有
时有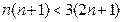 ,
,
所以当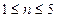
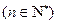 时有
时有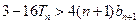 ………………………13分
………………………13分
综上:当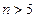
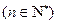 时有
时有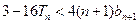 ;
;
当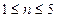
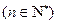 时有
时有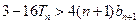 ………………………14分
………………………14分
 得:
得: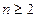 时,
时,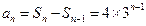 ………………………2分
………………………2分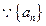 是等比数列,
是等比数列,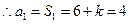
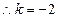 ,
,得
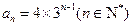 ……4分
……4分(Ⅱ)由
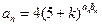 和
和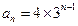 得
得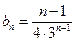 ……………………6分
……………………6分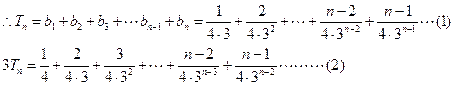
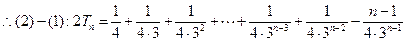
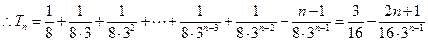 ……10分
……10分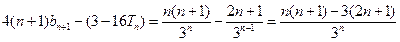
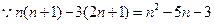 ………………………11分
………………………11分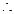 当
当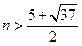 或
或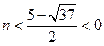 时有
时有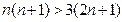 ,
,所以当
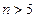
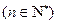 时有
时有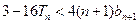
那么同理可得:当
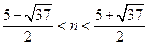 时有
时有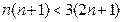 ,
,所以当
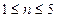
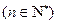 时有
时有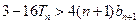 ………………………13分
………………………13分综上:当
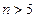
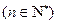 时有
时有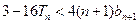 ;
;当
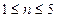
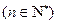 时有
时有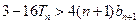 ………………………14分
………………………14分
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
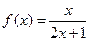 ,数列
,数列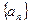 满足
满足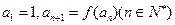 .
.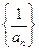 是等差数列;(Ⅱ)记
是等差数列;(Ⅱ)记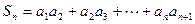 ,试比较
,试比较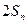 与1的大小.
与1的大小.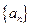 的前项和为
的前项和为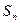 ,且
,且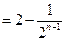 ,
,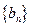 为等差数列,且
为等差数列,且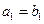 ,
,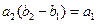 .
.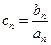 ,求数列
,求数列 的前
的前 项和
项和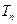 .
.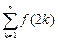 = 。
= 。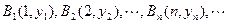 (
(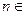 N
N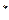 )顺次为直线
)顺次为直线 上的点,点
上的点,点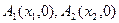
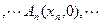 (
(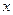 轴上的点,其中
轴上的点,其中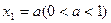 ,对任意的
,对任意的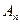 、
、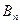 、
、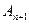 构成以
构成以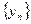 是等差数列;(Ⅱ)求证:对任意的
是等差数列;(Ⅱ)求证:对任意的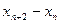 是常数,并求数列
是常数,并求数列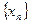 的通项公式; (Ⅲ)在上述等腰三角形
的通项公式; (Ⅲ)在上述等腰三角形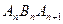 中是否存在直角三角形,若存在,求出此时
中是否存在直角三角形,若存在,求出此时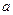 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 的前n项和为
的前n项和为 ,令
,令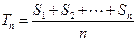 ,称
,称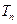 为数列
为数列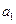 ,
,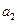 ,……,
,……,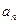 的“理想数”,已知数列
的“理想数”,已知数列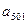 的“理想数”为2008,那么数列2,
的“理想数”为2008,那么数列2,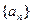 是等差数列,则( )
是等差数列,则( )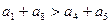 B
B 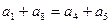
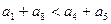 D
D 
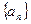 和
和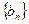 的前
的前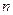 项和分别为
项和分别为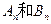 ,且
,且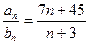 则
则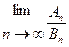 为( )
为( )