题目内容
设数列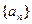 的通项公式为
的通项公式为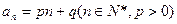 。数列
。数列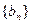 定义如下:对于正整数m,
定义如下:对于正整数m,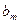 是使得不等式
是使得不等式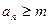 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若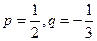 ,求b3; (2)若
,求b3; (2)若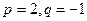 ,求数列
,求数列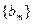 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得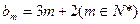 ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
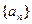 的通项公式为
的通项公式为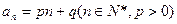 。数列
。数列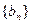 定义如下:对于正整数m,
定义如下:对于正整数m,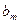 是使得不等式
是使得不等式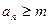 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若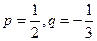 ,求b3; (2)若
,求b3; (2)若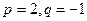 ,求数列
,求数列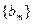 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得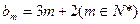 ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。(Ⅰ) 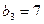 (Ⅱ)
(Ⅱ) 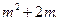 (Ⅲ)
(Ⅲ)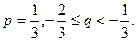
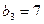 (Ⅱ)
(Ⅱ) 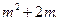 (Ⅲ)
(Ⅲ)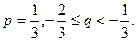
(1)由题意:得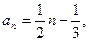 解
解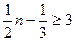 ,得
,得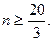
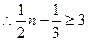 成立的所有n中的最小整数为7,即
成立的所有n中的最小整数为7,即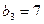 …4分
…4分
(2)由题意,得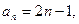 对于正整数,由
对于正整数,由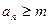 ,
,
得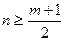 .根据
.根据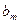 的定义可知当
的定义可知当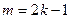 时,
时,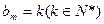 ;
;
当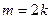 时,
时,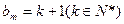 ;………3分
;………3分
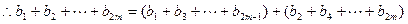
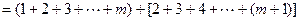
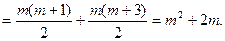 ………2分
………2分
(3)假设存在p和q满足条件,由不等式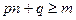 及
及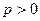 得
得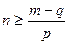 .
.
 ,根据
,根据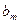 的定义可知,对于任意的正整数m都有
的定义可知,对于任意的正整数m都有
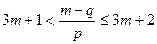 ,即
,即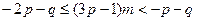 对任意的正整数m都成立。当
对任意的正整数m都成立。当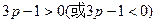 时,得
时,得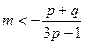 (或
(或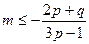 ),
),
这与上述结论矛盾:当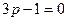 ,即
,即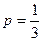 时,得
时,得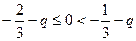 ,
,
角得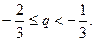 …4分∴存在p和q,使得
…4分∴存在p和q,使得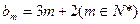 ;
;
p和q的取值范围分别是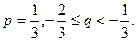 ………1分
………1分
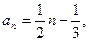 解
解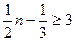 ,得
,得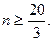
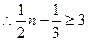 成立的所有n中的最小整数为7,即
成立的所有n中的最小整数为7,即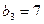 …4分
…4分(2)由题意,得
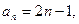 对于正整数,由
对于正整数,由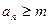 ,
,得
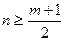 .根据
.根据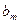 的定义可知当
的定义可知当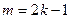 时,
时,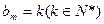 ;
;当
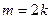 时,
时,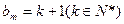 ;………3分
;………3分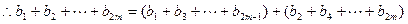
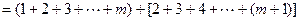
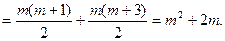 ………2分
………2分(3)假设存在p和q满足条件,由不等式
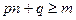 及
及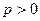 得
得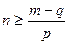 .
. ,根据
,根据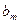 的定义可知,对于任意的正整数m都有
的定义可知,对于任意的正整数m都有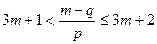 ,即
,即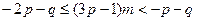 对任意的正整数m都成立。当
对任意的正整数m都成立。当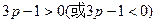 时,得
时,得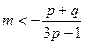 (或
(或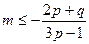 ),
),这与上述结论矛盾:当
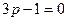 ,即
,即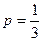 时,得
时,得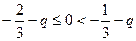 ,
,角得
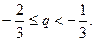 …4分∴存在p和q,使得
…4分∴存在p和q,使得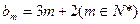 ;
;p和q的取值范围分别是
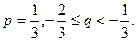 ………1分
………1分
练习册系列答案
相关题目
 次操作后剩余图形的总面积为
次操作后剩余图形的总面积为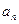
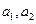 ;(2)求第
;(2)求第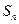 ;
; 中,
中,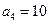 且
且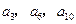 成等比数列,求数列
成等比数列,求数列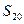 .
.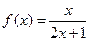 ,数列
,数列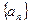 满足
满足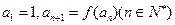 .
.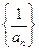 是等差数列;(Ⅱ)记
是等差数列;(Ⅱ)记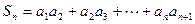 ,试比较
,试比较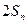 与1的大小.
与1的大小.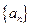 的前项和为
的前项和为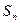 ,且
,且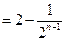 ,
,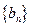 为等差数列,且
为等差数列,且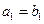 ,
,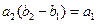 .
.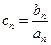 ,求数列
,求数列 的前
的前 项和
项和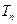 .
.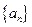 是等差数列,
是等差数列, 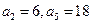 ;数列
;数列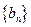 的前n项和是
的前n项和是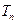 ,且
,且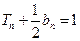 .
.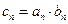 ,求
,求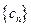 的前n项和
的前n项和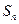 .
.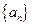 的前
的前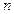 项和为
项和为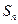 ,若
,若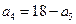 ,则
,则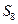 等于 ()
等于 ()