题目内容
求适合下列条件的椭圆的标准方程:
(1)两个焦点坐标分别为(-4,0)和(4,0),且椭圆经过点(5,0);
(2)焦点在y轴上,且经过两个点(0,2)和(1,0);
(3)经过P(-2 ,1),Q(
,1),Q( ,-2)两点.
,-2)两点.
(1)两个焦点坐标分别为(-4,0)和(4,0),且椭圆经过点(5,0);
(2)焦点在y轴上,且经过两个点(0,2)和(1,0);
(3)经过P(-2
 ,1),Q(
,1),Q( ,-2)两点.
,-2)两点.(1)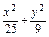 =1(2)
=1(2) +x2=1(3)
+x2=1(3)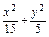 =1
=1
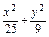 =1(2)
=1(2) +x2=1(3)
+x2=1(3)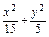 =1
=1 (1)由于椭圆的焦点在x轴上,所以设它的标准方程为 =1(a>b>0).
=1(a>b>0).
∴2a=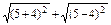 =10,
=10,
∴a=5.又c=4,∴b2=a2-c2=25-16=9.
故所求椭圆的方程为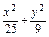 =1.
=1.
(2)由于椭圆的焦点在y轴上,所以设它的标准方程为
 ="1" (a>b>0).
="1" (a>b>0).
由于椭圆经过点(0,2)和(1,0),
∴ ∴
∴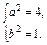 故所求椭圆的方程为
故所求椭圆的方程为 +x2=1.
+x2=1.
(3)设椭圆的标准方程为
mx2+ny2="1" (m>0,n>0,m≠n),点P(-2 ,1),Q(
,1),Q( ,-2)在椭圆上,
,-2)在椭圆上,
代入上述方程得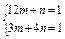 解得
解得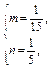 ∴
∴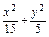 =1.
=1.
 =1(a>b>0).
=1(a>b>0).∴2a=
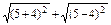 =10,
=10,∴a=5.又c=4,∴b2=a2-c2=25-16=9.
故所求椭圆的方程为
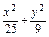 =1.
=1.(2)由于椭圆的焦点在y轴上,所以设它的标准方程为
 ="1" (a>b>0).
="1" (a>b>0).由于椭圆经过点(0,2)和(1,0),
∴
 ∴
∴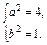 故所求椭圆的方程为
故所求椭圆的方程为 +x2=1.
+x2=1.(3)设椭圆的标准方程为
mx2+ny2="1" (m>0,n>0,m≠n),点P(-2
 ,1),Q(
,1),Q( ,-2)在椭圆上,
,-2)在椭圆上,代入上述方程得
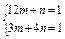 解得
解得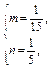 ∴
∴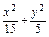 =1.
=1.
练习册系列答案
相关题目
 +
+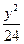 =1上一点P与椭圆两焦点F1、F2,连线的夹角为直角,则|PF1|·|PF2|=_________.
=1上一点P与椭圆两焦点F1、F2,连线的夹角为直角,则|PF1|·|PF2|=_________. 中,已知
中,已知 ,且当顶点
,且当顶点 位于定点
位于定点 时,
时, 有最小值为
有最小值为 .(1)建立适当的坐标系,求顶点
.(1)建立适当的坐标系,求顶点 作直线与(1)中的曲线交于
作直线与(1)中的曲线交于 、
、 两点,求
两点,求 的最小值的集合.
的最小值的集合. ,1)、P2(-
,1)、P2(- ,-
,- ),求椭圆的方程.
),求椭圆的方程. 左右焦点分别为
左右焦点分别为 、
、 ,点
,点 在椭圆上,若
在椭圆上,若 轴的距离为( )
轴的距离为( ) B 3 C
B 3 C  D
D 
 d,
d, ≤d≤
≤d≤ .
. ·
· =
= ,求向量
,求向量 与
与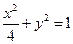 上一点A到左焦点的距离为
上一点A到左焦点的距离为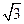 ,则点A到直线
,则点A到直线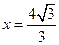 的距离为( )
的距离为( )



 。
。 ,
, ,则
,则 的轨迹方程是
的轨迹方程是