题目内容
已知点F(1，0)，直线l:x=2.设动点P到直线l的距离为d,且|PF|=
d,
≤d≤
.
(1)求动点P的轨迹方程；
(2)若
·
=
，求向量
与的夹角.
d,≤d≤.(1)求动点P的轨迹方程；
(2)若
·=，求向量与的夹角.(1) 轨迹方程为
+y2=1(
≤x≤
).
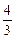(2)θ=arccos
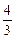+y2=1(≤x≤).(2)θ=arccos(1)根据椭圆的第二定义知，点P的轨迹为椭圆.由条件知c=1,
=2,∴a=
.
e=
=
=满足|PF|=d.
∴P点的轨迹为+
=1.
又d=－x,且≤d≤,
∴≤2－x≤.∴≤x≤.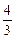
∴轨迹方程为+y2=1(≤x≤).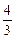
(2)由(1)可知，P点的轨迹方程为+y2=1(≤x≤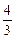),∴F(1,0)、P(x0,y0).
=(1,0),=(x0,y0),=(1－x0,－y0).
∵·=,∴1－x0=.
∴x0=,y0=±
.
又·=||·||·cosθ,
∴1·x0+0·y0=
·1·cosθ.
∴cosθ=
=
=
=.
∴θ=arccos.
=2,∴a=.e=
==满足|PF|=d.∴P点的轨迹为
+=1.又d=
－x,且≤d≤,∴
≤2－x≤.∴≤x≤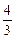.∴轨迹方程为
+y2=1(≤x≤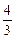).(2)由(1)可知，P点的轨迹方程为
+y2=1(≤x≤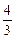),∴F(1,0)、P(x0,y0).=(1,0),=(x0,y0),=(1－x0,－y0).∵
·=,∴1－x0=.∴x0=
,y0=±.又
·=||·||·cosθ,∴1·x0+0·y0=
·1·cosθ.∴cosθ=
===.∴θ=arccos
.
练习册系列答案
相关题目
=
.
,
,
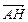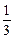
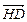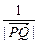能成等差数列吗?若能,求出M点的坐标；若不能,请说明理由.
，1），Q（
相的中心在原点，焦点在x轴上，离心率为
，点F1、F2分别是椭圆的左、右焦点，
与椭圆C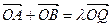
（O为坐标原点），求实数
的取值范围。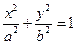
（
），其离心率为
，两准线之间的距离为
。（1）求
之值；（2）设点A坐标为(6, 0)，B为椭圆C上的动点，以A为直角顶点，作等腰直角△ABP（字母A，B，P按顺时针方向排列），求P点的轨迹方程。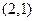
点，则该椭圆的半长轴长的取值范围是
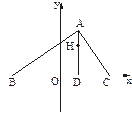
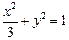上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是 ．
