题目内容
(1)已知椭圆以坐标轴为对称轴,且长轴是短轴的3倍,并且过点P(3,0),求椭圆的方程;
(2)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点P1( ,1)、P2(-
,1)、P2(- ,-
,- ),求椭圆的方程.
),求椭圆的方程.
(2)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点P1(
 ,1)、P2(-
,1)、P2(- ,-
,- ),求椭圆的方程.
),求椭圆的方程.(1)椭圆的方程为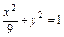 或
或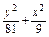 =1(2)
=1(2)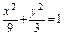
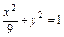 或
或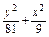 =1(2)
=1(2)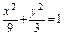
(1)若焦点在x轴上,设方程为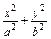 ="1" (a>b>0).
="1" (a>b>0).
∵椭圆过P(3,0),∴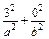 =1.
=1.
又2a=3×2b,∴a=3,b=1,方程为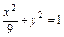 .
.
若焦点在y轴上,设方程为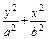 =1(a>b>0).
=1(a>b>0).
∵椭圆过点P(3,0),∴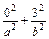 =1
=1
又2a=3×2b,∴a=9,b=3.∴方程为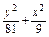 ="1."
="1."
∴所求椭圆的方程为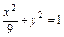 或
或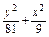 =1.
=1.
(2)设椭圆方程为mx2+ny2=1(m>0,n>0且m≠n).
∵椭圆经过P1、P2点,∴P1、P2点坐标适合椭圆方程,则 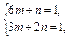
①、②两式联立,解得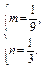
∴所求椭圆方程为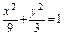 .
.
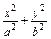 ="1" (a>b>0).
="1" (a>b>0).∵椭圆过P(3,0),∴
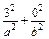 =1.
=1.又2a=3×2b,∴a=3,b=1,方程为
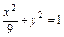 .
.若焦点在y轴上,设方程为
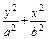 =1(a>b>0).
=1(a>b>0).∵椭圆过点P(3,0),∴
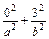 =1
=1又2a=3×2b,∴a=9,b=3.∴方程为
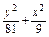 ="1."
="1." ∴所求椭圆的方程为
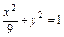 或
或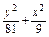 =1.
=1.(2)设椭圆方程为mx2+ny2=1(m>0,n>0且m≠n).
|
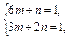
①、②两式联立,解得
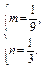
∴所求椭圆方程为
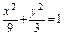 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
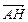 =
=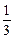
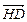 .
.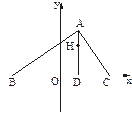
 ,
,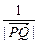 ,
, 能成等差数列吗?若能,求出M点的坐标;若不能,请说明理由.
能成等差数列吗?若能,求出M点的坐标;若不能,请说明理由.



 到两点
到两点 ,写出椭圆
,写出椭圆 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段 的中点
的中点 的轨迹方程;
的轨迹方程; 是椭圆
是椭圆 与椭圆相交于
与椭圆相交于 ,
, 两点,当直线
两点,当直线 ,
, 的斜率都存在,并记为
的斜率都存在,并记为 ,
, ,试探究
,试探究 的值是否与点
的值是否与点 的两个焦点为
的两个焦点为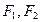 ,点
,点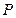 在椭圆
在椭圆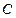 上,
上,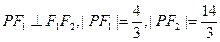 ,
,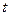 的取值范围,使得椭圆上有两个不同的点关于直线
的取值范围,使得椭圆上有两个不同的点关于直线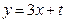 对称.
对称. 上任一点P,作椭圆C的右准线的垂线PH(H为垂足),延长PH到点Q,使|HQ|=λ|PH|(λ≥1)。当点P在椭圆C上运动时,点Q的轨迹的离心率的取值范围为( )
上任一点P,作椭圆C的右准线的垂线PH(H为垂足),延长PH到点Q,使|HQ|=λ|PH|(λ≥1)。当点P在椭圆C上运动时,点Q的轨迹的离心率的取值范围为( )




 ,1),Q(
,1),Q( k)
k)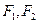 是椭圆的两个焦点,
是椭圆的两个焦点,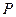 是椭圆上一点,若
是椭圆上一点,若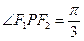 ,证明:
,证明: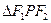 的面积只与椭圆的短轴长有关
的面积只与椭圆的短轴长有关 ,
, 是椭圆上一点,且
是椭圆上一点,且 是
是 ,
, 的等差中项,则椭圆的标准方程是( ).
的等差中项,则椭圆的标准方程是( ).


