题目内容
椭圆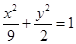 的焦点为
的焦点为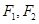 ,点
,点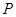 在椭圆上,若
在椭圆上,若 ,
,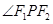 的大小为 .
的大小为 .
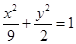 的焦点为
的焦点为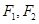 ,点
,点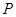 在椭圆上,若
在椭圆上,若 ,
,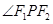 的大小为 .
的大小为 .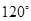
试题分析:根据椭圆的方程椭圆
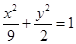 ,可知
,可知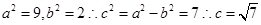
那么在
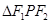 中,结合余弦定理,
中,结合余弦定理,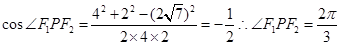 可知
可知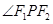 的大小为
的大小为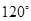 。故答案为
。故答案为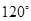 。
。点评:解决该试题的关键是利用椭圆的定义,以及椭圆的性质,表示出焦点三角形三边,求解得到角,属于基础题。

练习册系列答案
相关题目
题目内容
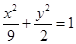 的焦点为
的焦点为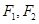 ,点
,点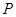 在椭圆上,若
在椭圆上,若 ,
,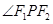 的大小为 .
的大小为 .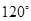
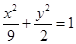 ,可知
,可知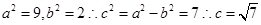
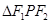 中,结合余弦定理,
中,结合余弦定理,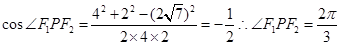 可知
可知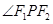 的大小为
的大小为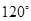 。故答案为
。故答案为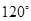 。
。