题目内容
已知椭圆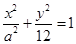 的一个焦点与抛物线
的一个焦点与抛物线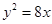 的焦点重合,则该椭圆的离心率为( )
的焦点重合,则该椭圆的离心率为( )
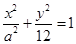 的一个焦点与抛物线
的一个焦点与抛物线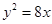 的焦点重合,则该椭圆的离心率为( )
的焦点重合,则该椭圆的离心率为( )A.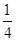 | B.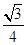 | C.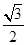 | D.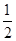 |
D
试题分析:抛物线
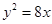 的焦点为(2,0),所以
的焦点为(2,0),所以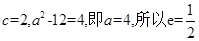 。
。点评:熟记椭圆中a、b、c的关系式,不要和双曲线中a、b、c的关系式弄混淆了。属于基础题型。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
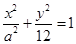 的一个焦点与抛物线
的一个焦点与抛物线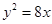 的焦点重合,则该椭圆的离心率为( )
的焦点重合,则该椭圆的离心率为( )A.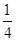 | B.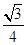 | C.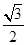 | D.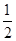 |
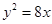 的焦点为(2,0),所以
的焦点为(2,0),所以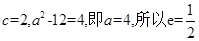 。
。
 阅读快车系列答案
阅读快车系列答案