题目内容
若正三角形的一个顶点在原点,另两个顶点在抛物线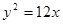 上,则这个三角形的面积为 。
上,则这个三角形的面积为 。
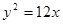 上,则这个三角形的面积为 。
上,则这个三角形的面积为 。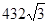
试题分析:设正三角形在第一象限的点为
 ,由正三角形性质可得
,由正三角形性质可得 ,点在抛物线上得
,点在抛物线上得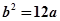

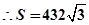
点评:本题利用抛物线的对称性可知正三角形两顶点关于x轴对称,因此求得
 即可得到三角形的边长
即可得到三角形的边长
练习册系列答案
相关题目
题目内容
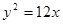 上,则这个三角形的面积为 。
上,则这个三角形的面积为 。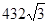
 ,由正三角形性质可得
,由正三角形性质可得 ,点在抛物线上得
,点在抛物线上得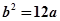

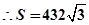
 即可得到三角形的边长
即可得到三角形的边长