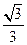题目内容
(本小题满分14分)
设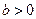 ,椭圆方程为
,椭圆方程为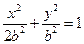 ,抛物线方程为
,抛物线方程为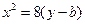 .如图6所示,过点
.如图6所示,过点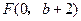 作
作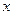 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为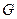 ,已知抛物线在点
,已知抛物线在点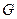 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点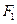 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设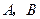 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点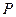 ,使得
,使得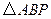 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).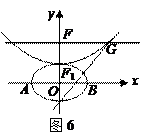
设
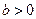 ,椭圆方程为
,椭圆方程为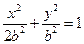 ,抛物线方程为
,抛物线方程为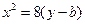 .如图6所示,过点
.如图6所示,过点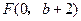 作
作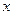 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为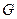 ,已知抛物线在点
,已知抛物线在点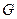 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点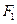 .
.(1)求满足条件的椭圆方程和抛物线方程;
(2)设
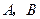 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点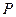 ,使得
,使得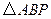 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).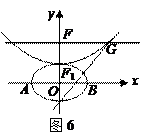
(1)由
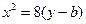 得
得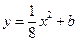
当
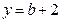 时,
时,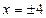 ,
,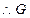 点的坐标为
点的坐标为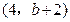
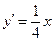 ,
,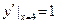
过点
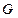 的切线方程为
的切线方程为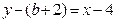 ,即
,即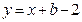 ,
,令
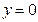 得
得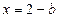 ,
,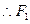 点的坐标为
点的坐标为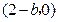 ;
;由椭圆方程得
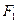 点的坐标为
点的坐标为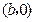 ,
,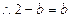 ,即
,即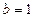 ,
,因此所求的椭圆方程及抛物线方程分别为
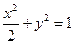 和
和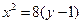 .
.(2)
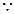 过
过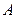 作
作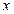 轴的垂线与抛物线只有一个交点
轴的垂线与抛物线只有一个交点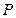 ,
,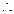 以
以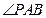 为直角的
为直角的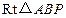 只有一个,
只有一个,同理以
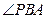 为直角的
为直角的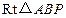 只有一个;
只有一个;若以
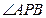 为直角,设
为直角,设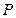 点的坐标为
点的坐标为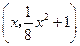 ,则
,则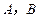 坐标分别为
坐标分别为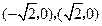
由
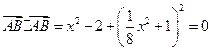 得
得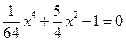 ,
,关于
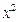 的一元二次方程有一解,
的一元二次方程有一解,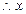 有二解,即以
有二解,即以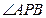 为直角的
为直角的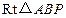 有二个;
有二个;因此抛物线上共存在4个点使
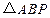 为直角三角形.
为直角三角形.考查椭圆的、抛物线的方程,图形及其简单的几何性质,直线和圆锥曲线的位置关系,运算能力,分析、解决问题的能力.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
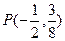 和到直线
和到直线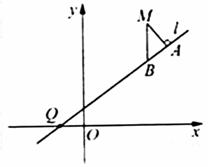
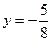 距离相等的点的轨迹,l是过点Q(-1,0)的直线,
距离相等的点的轨迹,l是过点Q(-1,0)的直线,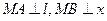
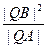 为常数。
为常数。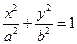
 的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行。又抛物线与椭圆交于点
的中心.椭圆的离心率是抛物线离心率的一半,且它们的准线互相平行。又抛物线与椭圆交于点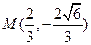 ,求抛物线与椭圆的方程.
,求抛物线与椭圆的方程.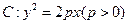 上任意一点到焦点F的距离比到
上任意一点到焦点F的距离比到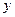 轴的距离大1,(1)求抛物线C的方程;(2)若过焦点F的直线交抛物线于M,N两点,M在第一象限,且
轴的距离大1,(1)求抛物线C的方程;(2)若过焦点F的直线交抛物线于M,N两点,M在第一象限,且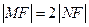 ,求直线MN的方程;(3)过点
,求直线MN的方程;(3)过点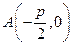 的直线交抛物线
的直线交抛物线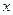 轴的对称点为R,求证:直线RQ必过定点.
轴的对称点为R,求证:直线RQ必过定点.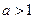 ,则双曲线
,则双曲线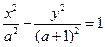 的离心率
的离心率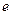 的取值范围是( )
的取值范围是( )
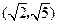
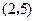
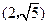
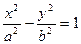 的离心率为
的离心率为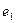 ,双曲线
,双曲线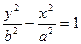 的离心率为
的离心率为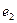 ,则
,则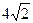
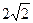
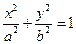
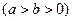 的左、右焦点分别为
的左、右焦点分别为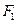 、
、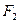 ,抛物线
,抛物线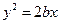 的焦点为
的焦点为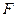 .若
.若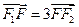 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )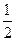 B.
B.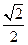 C.
C.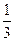 D.
D.