题目内容
【题目】已知函数![]() 在点
在点![]() 处取得极值
处取得极值![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 有极大值
有极大值![]() ,求
,求![]() 在
在![]() 上的最小值.
上的最小值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1) 函数![]() 在点
在点![]() 处取得极值
处取得极值![]() ,则
,则![]() ,
, ![]() ,列方程组解出a,b的值即可;(2)对函数求导判断单调性,求出函数的极大值,由极大值
,列方程组解出a,b的值即可;(2)对函数求导判断单调性,求出函数的极大值,由极大值![]() 可求出c的值,代回解析式,根据单调性求出函数
可求出c的值,代回解析式,根据单调性求出函数![]() 在
在![]() 上的最小值.
上的最小值.
试题解析:
(1)因f(x)=ax3+bx+c,故f′(x)=3ax2+b,
由于f(x)在点x=2处取得极值c-16,
故有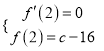 ,
,
即![]() 化简得
化简得![]() ,
,
解得a=1,b=-12.
(2)由(1)知f(x)=x3-12x+c;
f′(x)=3x2-12=3(x-2)(x+2).
令f′(x)=0,得x1=-2,x2=2.
当x∈(-∞,-2)时,f′(x)>0,故f(x)在(-∞,-2)上为增函数;
当x∈(-2,2)时,f′(x)<0,故f(x)在(-2,2)上为减函数;
当x∈(2,+∞)时,f′(x)>0,
故f(x)在(2,+∞)上为增函数.
由此可知f(x)在x1=-2处取得极大值f(-2)=16+c,f(x)在x1=2处取得极小值f(2)=c-16.
由题设条件知16+c=28得c=12.
此时f(-3)=9+c=21,f(3)=-9+c=3,
f(2)=-16+c=-4,
因此f(x)在[-3,3]上的最小值为f(2)=-4.
点睛: 函数的导数与极值点的关系:(1)定义域![]() 上的可导函数
上的可导函数![]() 在
在![]() 处取得极值的充要条件是
处取得极值的充要条件是![]() ,并且
,并且![]() 在
在![]() 两侧异号,若左负右正为极小值点,若左正右负为极大值点;(2)函数
两侧异号,若左负右正为极小值点,若左正右负为极大值点;(2)函数![]() 在点
在点![]() 处取得极值时,它在这点的导数不一定存在,例如函数
处取得极值时,它在这点的导数不一定存在,例如函数![]() ,结合图象,知它在
,结合图象,知它在![]() 处有极小值,但它在
处有极小值,但它在![]() 处的导数不存在;(3)
处的导数不存在;(3) ![]() 既不是函数
既不是函数![]() 在
在![]() 处取得极值的充分条件也不是必要条件.最后一定要注意对极值点进行检验.
处取得极值的充分条件也不是必要条件.最后一定要注意对极值点进行检验.

练习册系列答案
相关题目