题目内容
【题目】如图(1)所示,已知四边形![]() 是由直角△
是由直角△![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]()
![]() .且点
.且点![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() 现将△
现将△![]() 沿
沿![]() 进行翻折,使得二面角
进行翻折,使得二面角![]()
![]() 的大小为
的大小为![]() ,得到图形如图(2)所示,连接
,得到图形如图(2)所示,连接![]() ,点
,点![]() 分别在线段
分别在线段![]() 上.
上.


(1)证明: ![]() ;
;
(2)若三棱锥![]() 的体积为四棱锥
的体积为四棱锥![]() 体积的
体积的![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)直二面角定义可得![]() ,再根据已知条件
,再根据已知条件![]() ,由线面垂直判定定理得
,由线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() ;另一方面,由计算可得
;另一方面,由计算可得![]() ;因此由线面垂直判定定理得
;因此由线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() .(2)利用等体积法,将三棱锥
.(2)利用等体积法,将三棱锥![]() 的体积转化为
的体积转化为![]() ,再根据椎体体积公式得
,再根据椎体体积公式得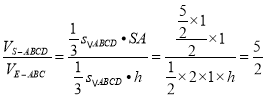 ,解得
,解得![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:(Ⅰ)证明:因为二面角![]() 的大小为
的大小为![]() ,则
,则![]() ,
,
又![]() ,故
,故![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ;
;
在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,又
,又![]() ,
,
所以![]() ,即
,即![]() ;又
;又![]() ,故
,故![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,故
,故![]() .
.
(Ⅱ)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,因为
,因为![]() ,且
,且![]() ,
,
故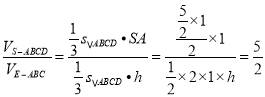 ,
,
故![]() ,做点
,做点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目