题目内容
【题目】已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜ 
）的部分图象如图所示． 
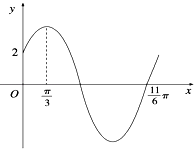
（1）求f（x）的解析式；
（2）将函数y=f（x）的图象上所有点的纵坐标不变，横坐标缩短为原来的 
倍，再将所得函数图象向右平移 
个单位，得到函数y=g（x）的图象，求g（x）的单调递增区间；
（3）当x∈[﹣ ， 
]时，求函数y=f（x+ 
）﹣ 
f（x+ 
）的最值．
【答案】
（1）解：由图可得， 
，
∴T=2π，则 
．
由五点作图的第二点知， 
φ= 
，则φ= 
．
∴f（x）=Asin（x+ ），
又f（0）=Asin =2，得A=4．
∴f（x）=4sin（x+ ）
（2）解：将函数y=f（x）的图象上所有点的纵坐标不变，横坐标缩短为原来的 
倍所得函数解析式
为y=4sin（2x+ ），再将所得函数图象向右平移 个单位，解析式变为y=4sin[2（x﹣ ）+ ]，
∴g（x）=4sin（2x﹣ ）．
由 
，解得： 
．
∴g（x）的单调递增区间为 
（3）解：y=f（x+ 
）﹣ 
f（x+ 
）
=4sin（x+ + ）﹣4 sin（x+ + ）
=4sin（x+ 
）﹣4 cosx
=4sinxcos +4cosxsin ﹣ 
=4sin（x﹣ ）．
∵x∈[﹣ ， 
]，
∴ 
，
∴函数y=f（x+ ）﹣ f（x+ ）的最小值为﹣4，最大值为2．
【解析】（1）由图得到函数的四分之三周期，进一步求得周期，代入周期公式求ω，然后利用五点作图的第二点求得φ，再由f（0）=2求得A的值，则函数解析式可求；（2）由函数的周期变化和平移变换求得g（x），然后再由简单的复合函数单调性的求法求解g（x）的增区间；（3）结合（1）中的f（x）的解析式求得y=f（x+ ）﹣ f（x+ ），利用三角恒等变换变形后根据x的范围求最值．
【题目】【2015高考福建文数】全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标．根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据，对名列前20名的“省级卫视新闻台”的融合指数进行分组统计，结果如表所示．
组号 | 分组 | 频数 |
1 | | 2 |
2 | | 8 |
3 | | 7 |
4 | | 3 |
（Ⅰ）现从融合指数在
和
内的“省级卫视新闻台”中随机抽取2家进行调研，求至少有1家的融合指数在的概率；
（Ⅱ）根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数．
