题目内容
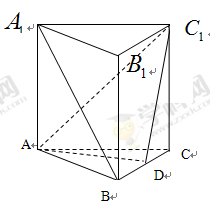
如图,已知直三棱柱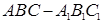 中,
中,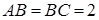 ,
,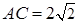 ,
,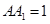 ,D为BC的中点.
,D为BC的中点.
(1)求证: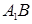 ∥面
∥面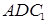 ;
;
(2)求三棱锥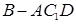 的体积.
的体积.
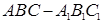 中,
中,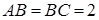 ,
,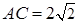 ,
,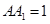 ,D为BC的中点.
,D为BC的中点.
(1)求证:
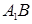 ∥面
∥面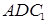 ;
;(2)求三棱锥
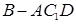 的体积.
的体积.(1)略(2)

试题分析:(1)连接交
 于点O,连接OD,在
于点O,连接OD,在 中可根据中位线证得
中可根据中位线证得 ∥
∥ ,再根据线面平行的性质定理可证得
,再根据线面平行的性质定理可证得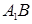 ∥面
∥面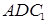 。(2)法一:因为
。(2)法一:因为 为
为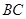 的中点,所以
的中点,所以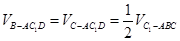 。法二:因为
。法二:因为 ,可转化为求
,可转化为求 。
。试题解析:解:(1)连接交
 于点O,连接OD,∵O、D分别为
于点O,连接OD,∵O、D分别为 、BC的中点,∴
、BC的中点,∴ ∥
∥ 且
且 =
= 又∵
又∵ 
 面
面 且
且
 面
面 ∴
∴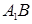 ∥面
∥面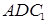 。(6分)
。(6分)(2)∵
 又∵
又∵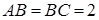 ,
,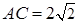 ,∴
,∴ 又∵
又∵ 为
为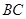 的中点∴BD=1∴
的中点∴BD=1∴ =
=  AB·BD=1。∵
AB·BD=1。∵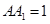 ∴
∴ ∴
∴ 。(12分)
。(12分)
练习册系列答案
相关题目
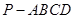 中,底面
中,底面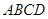 是菱形,
是菱形, ,
, ,
,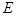 是
是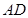 的中点,点
的中点,点 在侧棱
在侧棱 上.
上.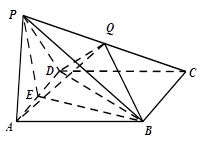
 ;
; //平面
//平面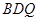 ;
; ,试求
,试求 的值.
的值.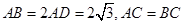 ,F是AB上的一点,且
,F是AB上的一点,且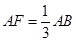 ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知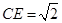
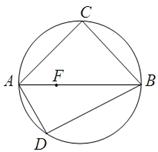
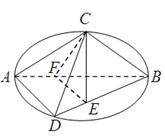
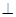 平面BCE
平面BCE ,则球的表面积为( )
,则球的表面积为( )




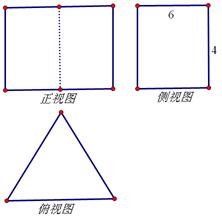
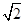 的正方形,则以该空间几何体各个面的中心为顶点的多面体的体积为( ).
的正方形,则以该空间几何体各个面的中心为顶点的多面体的体积为( ).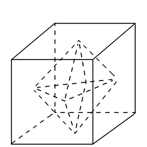
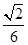
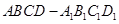 的外接球
的外接球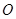 的体积为
的体积为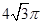 ,则球心
,则球心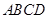 的距离为( )
的距离为( )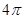 ,底面积为
,底面积为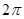 ,则该圆锥的母线长为 .
,则该圆锥的母线长为 .