题目内容
如图C,D是以AB为直径的圆上的两点,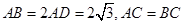 ,F是AB上的一点,且
,F是AB上的一点,且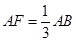 ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知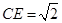
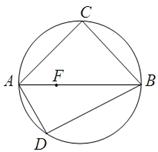
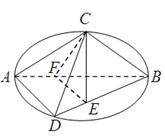
(1)求证:AD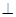 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
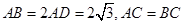 ,F是AB上的一点,且
,F是AB上的一点,且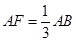 ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知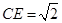


(1)求证:AD
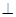 平面BCE
平面BCE(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
(1)参考解析;(2)参考解析;(3)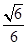
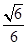
试题分析:(1)因为由于AB是圆的直径,所以AD⊥BD,又因为点C在平面ABD的射影E在BD上,所以CE⊥平面ADB.又因为
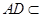 平面ADB.所以AD⊥CE.又因为
平面ADB.所以AD⊥CE.又因为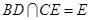 .所以AD⊥平面BCE.
.所以AD⊥平面BCE.(2)因为
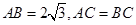 ,
,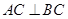 .有直角三角形的勾股定理可得
.有直角三角形的勾股定理可得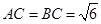 .在直角三角形BCE中,又
.在直角三角形BCE中,又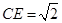 .所以
.所以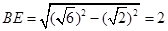 .又BD=3,
.又BD=3,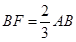 .所以可得
.所以可得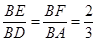 .所以AD∥FE,又因为
.所以AD∥FE,又因为 平面CEF,
平面CEF, 平面CE.所以AD//平面CEF.
平面CE.所以AD//平面CEF.(3)通过转换顶点三棱锥A-CFD的体积
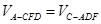 .因为
.因为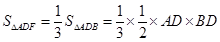
 .所以
.所以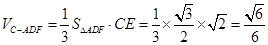 .
.试题解析:(1)证明:依题意:
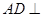
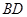

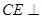 平面
平面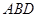 ∴
∴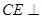


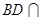
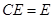 ∴
∴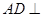 平面
平面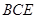 . 4分
. 4分(2)证明:
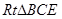 中,
中,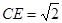 ,
,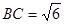 ∴
∴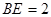
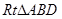 中,
中,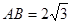 ,
,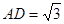 ∴
∴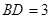 .
. ∴
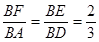 . ∴
. ∴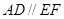

 在平面
在平面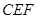 外,
外,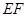 在平面
在平面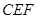 内,
内,∴
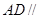 平面
平面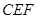 . 8分
. 8分(3)解:由(2)知
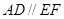 ,
,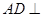
 ,且
,且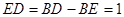

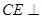 平面
平面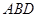
∴
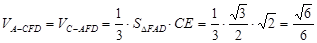 . 12分
. 12分
练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
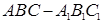 中,
中,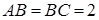 ,
,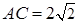 ,
,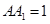 ,D为BC的中点.
,D为BC的中点.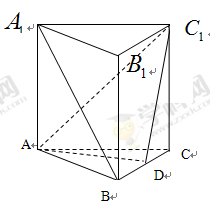
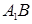 ∥面
∥面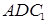 ;
;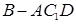 的体积.
的体积.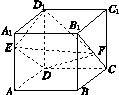
 纬线长度为
纬线长度为 cm,该地球仪的表面积为 cm2.
cm,该地球仪的表面积为 cm2.




 ,底面面积为
,底面面积为 ,一条侧棱长为
,一条侧棱长为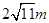 ,则它的侧面积为 .
,则它的侧面积为 . 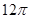 ,则圆锥侧面积等于___________.
,则圆锥侧面积等于___________.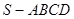 的所有棱长均为
的所有棱长均为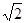 ,则过该棱锥的顶点
,则过该棱锥的顶点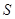 及底面正方形各边中点的球的体积为 .
及底面正方形各边中点的球的体积为 . 的半径为
的半径为 ,则球
,则球