题目内容
【题目】已知函数y=f（x）（x∈R）的图象如图所示，f′（x）是f（x）的导函数，则不等式（x﹣1）f′（x）＜0的解集为（ ）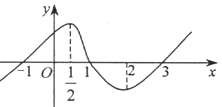 
A.（﹣∞， 
）∪（1，2）
B.（﹣1，1）∪（1，3）
C.（﹣1， ）∪（3，+∞）
D.（﹣∞，﹣1）∪（3，+∞）
【答案】A
【解析】解：当x﹣1＞0，即x＞1时，f'（x）＜0， 即找在f（x）在（1，+∞）上的减区间，
由图象得，1＜x＜2；
当x﹣1＜0时，即x＜1时，f'（x）＞0，
即找f（x）在（﹣∞，1）上的增区间，
由图象得，x＜ 
．
故不等式解集为（﹣∞， ）∪（1，2）
故选：A．
先由（x﹣1）f'（x）＜0，分成x﹣1＞0且f'（x）＜0或x﹣1＜0且f'（x）＞0两种情况分别讨论即可
练习册系列答案
相关题目
