题目内容
【题目】某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题: 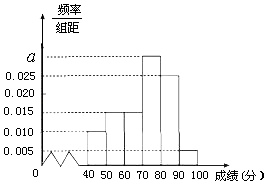
(1)求a并估计这次考试中该学科的中位数、平均值;
(2)现根据本次考试分数分成下列六段(从低分段到高分段依次为第一组、第二组…第六组)为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差不小于30分(以分数段为依据,不以具体学生分数为依据,如:[40,50),[70,80)这两组分数之差为30分),则称这两组为“最佳组合”,试求选出的两组为“最佳组合”的概率.
【答案】
(1)解:因为各组的频率和等于1,
故第四组的频率:
f4=1﹣(0.025+0.015×2+0.01+0.005)×10=0.3,∴a=0.03,
成绩在[40,70)的频率为:(0.01+0.015+0.015)×10=0.4,
成绩在[40,80)的频率为:0.4+0.03×10=0.7,
∴中位数在[70,80)内,
设中位数为x,
∵中位数要平分直方图的面积,
∴x=70+ ![]() =
= ![]() 分,
分,
依题意,60及以上的分数所在的第三、四、五、六组,
频率和为(0.015+0.03+0.025+0.005)×10=0.75
所以,抽样学生成绩的合格率是75%,
利用组中值估算抽样学生的平均分为:
45f1+55f2+65f3+75f4+85f5+95f6
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71
估计这次考试的平均分是71分
(2)解:记选出的两组为“最佳组合”为事件A.
从六组中任选两组的基本事件是:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),即n=5+4+3+2+1=15,符合“最佳组合”条件的有:(1,4),(1,5),(1,6),(2,5),(2,6),(3,6),即m=6, ![]()
所以,选出的两组为“最佳组合”的概率为 ![]()
【解析】(1)在频率分直方图中,小矩形的面积等于这一组的频率,根据频率的和等于1建立等式解之即可;由已知得中位数在[70,80)内,设中位数为x,由中位数要平分直方图的面积能求出结果;60及以上的分数所在的第三、四、五、六组,从而求出抽样学生成绩的合格率,再利用组中值估算抽样学生的平均分即可.(2)选出的两组为“最佳组合”的概所有的组合数有15个,其中,“最佳组合”有6个,由此求得选出的两组为“最佳组合”的概率.
【考点精析】认真审题,首先需要了解频率分布直方图(频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息).

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案