题目内容
设P是双曲线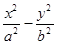 =1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是
=1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是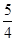 ,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )
,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )
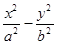 =1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是
=1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是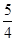 ,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )
,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )| A.4 | B.5 | C.6 | D.7 |
D
试题分析:由双曲线焦点三角形面积公式得
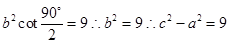 ,
,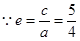
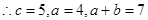
点评:双曲线
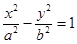 上一点P,则焦点三角形
上一点P,则焦点三角形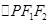 面积为
面积为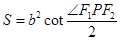

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 的直线交椭圆于A、B两点,若
的直线交椭圆于A、B两点,若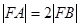 ,则椭圆的离心率为( )
,则椭圆的离心率为( )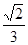 B.
B. 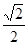 C.
C. 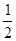 D.
D. 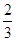
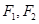 的椭圆
的椭圆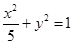 和双曲线
和双曲线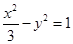 ,
,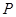 是它们的一个交点,则
是它们的一个交点,则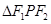 的形状是 ( )
的形状是 ( )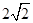 ,一个焦点的坐标为(1,0).
,一个焦点的坐标为(1,0).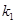 ,
,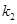 ,求证:
,求证: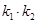 为定值.
为定值.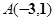 ,并且对称轴都在坐标轴上的等轴双曲线的方程为( )
,并且对称轴都在坐标轴上的等轴双曲线的方程为( )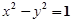
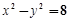

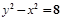
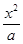 +
+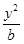 =1(
=1(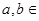 {1,2,3,4, ,2013})的曲线中,所有圆面积的和等于 ,离心率最小的椭圆方程为 .
{1,2,3,4, ,2013})的曲线中,所有圆面积的和等于 ,离心率最小的椭圆方程为 .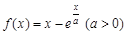 .
.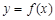 在
在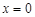 的切线能否与曲线
的切线能否与曲线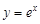 相切?并说明理由;
相切?并说明理由;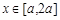 求
求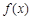 的最大值;
的最大值;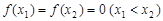 ,求证:
,求证: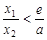 .
.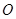 为原点,
为原点,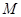 为动点,
为动点,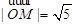 ,
,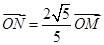 . 过点
. 过点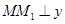 轴于
轴于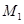 ,过
,过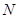 作
作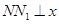 轴于点
轴于点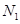 ,
,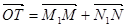 . 记点
. 记点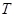 的轨迹为曲线
的轨迹为曲线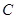 ,
,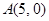 、
、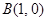 ,过点
,过点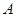 作直线
作直线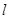 交曲线
交曲线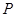 、
、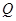 (点
(点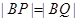 ,并说明理由.
,并说明理由. 为抛物线
为抛物线 的焦点,点
的焦点,点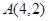 为抛物线内一定点,点
为抛物线内一定点,点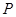 为抛物线上一动点,
为抛物线上一动点,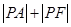 最小值为8.
最小值为8.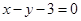 与抛物线交于
与抛物线交于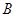 、
、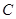 两点,求
两点,求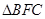 的面积.
的面积.