题目内容
已知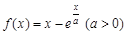 .
.
(Ⅰ)判断曲线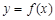 在
在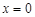 的切线能否与曲线
的切线能否与曲线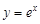 相切?并说明理由;
相切?并说明理由;
(Ⅱ)若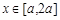 求
求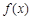 的最大值;
的最大值;
(Ⅲ)若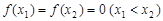 ,求证:
,求证: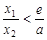 .
.
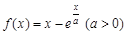 .
.(Ⅰ)判断曲线
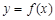 在
在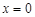 的切线能否与曲线
的切线能否与曲线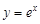 相切?并说明理由;
相切?并说明理由;(Ⅱ)若
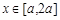 求
求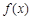 的最大值;
的最大值;(Ⅲ)若
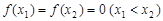 ,求证:
,求证: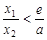 .
.(1)曲线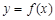 在
在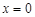 的切线不能与曲线
的切线不能与曲线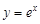 相切
相切
(2)当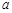 >
>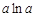 ,即
,即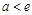 时,
时,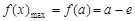 .
.
当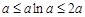 ,即
,即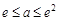 时,
时,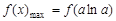 =
=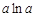
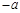 .
.
当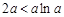 ,即
,即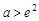 时,
时,
(3)构造函数结合导数的知识里求解最值,证明不等式。
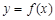 在
在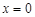 的切线不能与曲线
的切线不能与曲线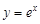 相切
相切(2)当
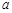 >
>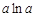 ,即
,即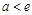 时,
时,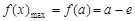 .
.当
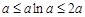 ,即
,即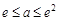 时,
时,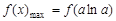 =
=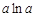
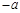 .
. 当
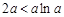 ,即
,即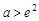 时,
时,
(3)构造函数结合导数的知识里求解最值,证明不等式。
试题分析:解:(Ⅰ)
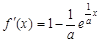 ,则
,则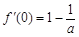 ,
,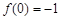 ,
,∴曲线
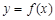 在
在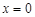 的切线l的方程为
的切线l的方程为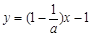 .
.若l与曲线
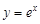 相切,设切点为
相切,设切点为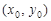 ,则
,则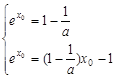 .
.由
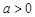 ,得
,得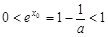 ,∴
,∴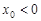 ,得
,得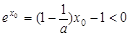 ,与
,与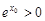 矛盾.
矛盾.∴曲线
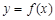 在
在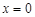 的切线不能与曲线
的切线不能与曲线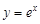 相切.
相切.(Ⅱ),令
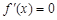 得
得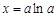 .
.∴
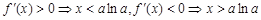 .
.∴
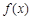 在
在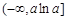 上为增函数,在
上为增函数,在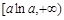 上为减函数.
上为减函数.∴当
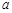 >
>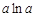 ,即
,即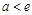 时,
时,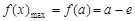 .
.当
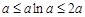 ,即
,即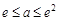 时,
时,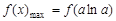 =
=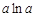
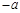 .
. 当
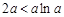 ,即
,即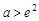 时,
时, .
. (Ⅲ)由(Ⅱ)知
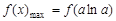 =
=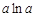
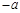 .
.∵
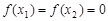 ,∴
,∴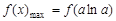 =
=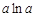
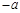
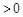 .
.∴
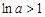 ,得
,得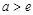 ,∴
,∴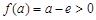 且
且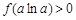 .
.得
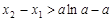 ,又
,又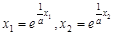 ,
,∴
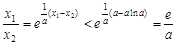 .
.点评:解决的关键是根据导数的符号判定函数的单调性,以及函数的最值,属于中档题。

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
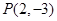 是双曲线
是双曲线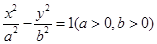 上一点,双曲线两个焦点间的距离等于4,则该双曲线方程是___________.
上一点,双曲线两个焦点间的距离等于4,则该双曲线方程是___________.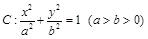 的左、右焦点分别为
的左、右焦点分别为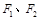 ,上顶点为
,上顶点为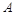 ,离心率为
,离心率为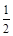 , 在
, 在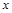 轴负半轴上有一点
轴负半轴上有一点 ,且
,且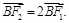
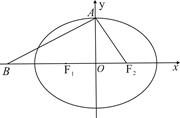
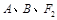 三点的圆 恰好与直线
三点的圆 恰好与直线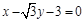 相切,求椭圆C的方程;
相切,求椭圆C的方程;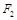 作斜率为
作斜率为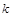 的直线
的直线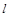 与椭圆C交于
与椭圆C交于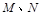 两点,在
两点,在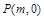 ,使得以
,使得以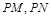 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出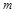 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.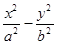 =1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是
=1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是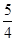 ,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )
,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )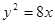 相切倾斜角为
相切倾斜角为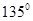 的直线
的直线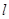 与
与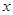 轴和
轴和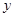 轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线
轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线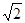 C.2 D.
C.2 D.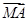 =λ
=λ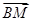 .
.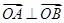 ;
; 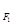 ,
,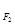 分别是椭圆E:
分别是椭圆E: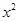 +
+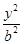 =1(0﹤b﹤1)的左、右焦点,过
=1(0﹤b﹤1)的左、右焦点,过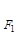 的直线
的直线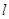 与E相交于A、B两点,且
与E相交于A、B两点,且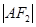 ,
,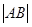 ,
,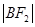 成等差数列。
成等差数列。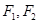 为椭圆
为椭圆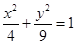 两个焦点,
两个焦点,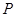 为椭圆上一点且
为椭圆上一点且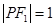 ,则
,则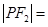 ( )
( )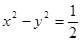 与椭圆有公共的焦点,且它们的离心率互为倒数,则该椭圆的标准方程为___________________。
与椭圆有公共的焦点,且它们的离心率互为倒数,则该椭圆的标准方程为___________________。