题目内容
已知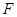 为抛物线
为抛物线 的焦点,点
的焦点,点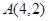 为抛物线内一定点,点
为抛物线内一定点,点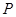 为抛物线上一动点,
为抛物线上一动点,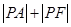 最小值为8.
最小值为8.
(1)求该抛物线的方程;
(2)若直线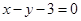 与抛物线交于
与抛物线交于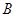 、
、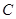 两点,求
两点,求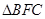 的面积.
的面积.
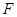 为抛物线
为抛物线 的焦点,点
的焦点,点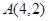 为抛物线内一定点,点
为抛物线内一定点,点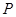 为抛物线上一动点,
为抛物线上一动点,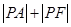 最小值为8.
最小值为8.(1)求该抛物线的方程;
(2)若直线
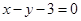 与抛物线交于
与抛物线交于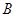 、
、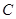 两点,求
两点,求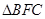 的面积.
的面积.(1)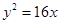 .(2)
.(2)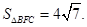
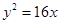 .(2)
.(2)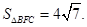
试题分析:(1)设
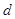 为点
为点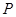 到
到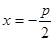 的距离,则由抛物线定义,
的距离,则由抛物线定义,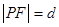 ,
,所以当点
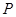 为过点
为过点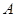 且垂直于准线的直线与抛物线的交点时,
且垂直于准线的直线与抛物线的交点时, 取得最小值,即
取得最小值,即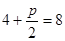 ,解得
,解得
∴抛物线的方程为
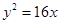 .
.(2)设
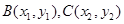 ,联立
,联立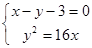 得
得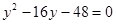 ,
,显然
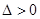 ,
,
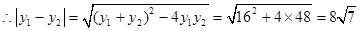 ,
,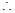
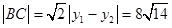 .
. 又

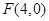 到直线
到直线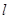 的距离为
的距离为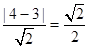 ,
,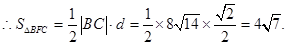
点评:中档题,涉及“抛物线内一定点,点
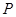 为抛物线上一动点,求
为抛物线上一动点,求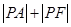 最小值”问题,往往利用抛物线定义,“化折为直”。涉及抛物线与直线位置关系问题,往往利用韦达定理。
最小值”问题,往往利用抛物线定义,“化折为直”。涉及抛物线与直线位置关系问题,往往利用韦达定理。
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
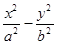 =1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是
=1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心 率是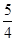 ,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )
,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )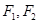 为椭圆
为椭圆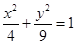 两个焦点,
两个焦点,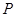 为椭圆上一点且
为椭圆上一点且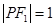 ,则
,则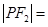 ( )
( )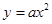 的准线方程为
的准线方程为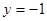 ,则实数
,则实数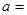 ( )
( )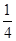
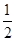
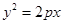 (p >0)的焦点F恰好是双曲线C2:
(p >0)的焦点F恰好是双曲线C2: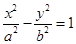 (a>0,b >0)的右焦点,且它们的交点的连线过点F,则双曲线的离心率为
(a>0,b >0)的右焦点,且它们的交点的连线过点F,则双曲线的离心率为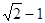
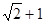
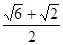
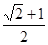
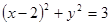 ,此圆与抛物线
,此圆与抛物线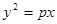
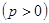 有四个不同的交点,若在
有四个不同的交点,若在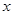 轴上方的两交点分别为
轴上方的两交点分别为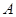 ,
,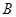 ,坐标原点为
,坐标原点为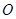 ,
,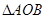 的面积为
的面积为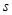 。
。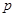 的取值范围;
的取值范围;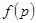 的表达式及
的表达式及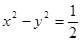 与椭圆有公共的焦点,且它们的离心率互为倒数,则该椭圆的标准方程为___________________。
与椭圆有公共的焦点,且它们的离心率互为倒数,则该椭圆的标准方程为___________________。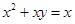 的曲线是( )
的曲线是( )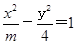 的右焦点与抛物线
的右焦点与抛物线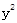 =12x的焦点重合,则m=______________.
=12x的焦点重合,则m=______________.