题目内容
18.已知抛物线y2=2px(p>0)的焦点为F,F关于原点的对称点为P.过F作x轴的垂线交抛物线于M、N两点.有下列四个命题:①△PMN必为直角三角形; ②△PMN不一定为直角三角形;③直线PM必与抛物线相切;
④直线PM不一定与抛物线相切.其中正确的命题是①③,(填序号)
分析 本题考查抛物线的定义和标准方程的有关知识,先由抛物线方程求出M,N的坐标,然后判断△PMN是否为为直角三角形,求出直线PM的方程,然后判断是否相切.
解答 解:抛物线方程为y2=2px(p>0),焦点为F($\frac{p}{2}$,0),则P点坐标为(-$\frac{p}{2}$,0),可求出点M($\frac{p}{2}$,p),N($\frac{p}{2}$,-p),
∴|PF|=$\frac{1}{2}$,|MN|=p,∴∠MPN=90°,故①正确,②不正确;
联立直线PM方程与抛物线方程:$\left\{\begin{array}{l}{y=x+\frac{p}{2}}\\{{y}^{2}=2px}\end{array}\right.$,得x2-px+$\frac{{p}^{2}}{4}$=0,其判别式△=0.
∴直线PM必与抛物线相切,故③正确,④不正确.
综上①③正确.
故答案为:①③.
点评 本题考查抛物线标准方程,考查抛物线的简单性质,解题关键是根据标准方程求出M,N坐标,是中档题.

练习册系列答案
相关题目
8.有7张卡片分别写有数字1,1,1,2,2,3,4,从中任取4张,可排出的四位数有( )个.
| A. | 78 | B. | 102 | C. | 114 | D. | 120 |
6.设复数$z=\frac{2}{-1-i}$,则$z•\overline z$=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
3.如图所示,在正方形OABC中任取一点,则该点落在阴影部分的概率为( )
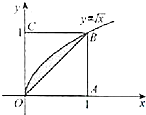

| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |