题目内容
8.有7张卡片分别写有数字1,1,1,2,2,3,4,从中任取4张,可排出的四位数有( )个.| A. | 78 | B. | 102 | C. | 114 | D. | 120 |
分析 根据题意,分四种情况讨论:①、取出的4张卡片中没有重复数字,即取出的4张卡片中的数字为1、2、3、4,②、取出的4张卡片中4有2个重复数字,则2个重复的数字为1或2,③若取出的4张卡片为2张1和2张2,④、取出的4张卡片种有3个重复数字,则重复的数字为1,分别求出每种情况下可以排出四位数的个数,由分类计数原理计算可得答案.
解答 解:根据题意,分四种情况讨论:
①、取出的4张卡片中没有重复数字,即取出的4张卡片中的数字为1、2、3、4,
此时有A44=24种顺序,可以排出24个四位数;
②、取出的4张卡片中有2个重复数字,则2个重复的数字为1或2,
若重复的数字为1,在2、3、4中取出2个,有C32=3种取法,安排在四个位置中,有A42=12种情况,剩余位置安排数字1,
可以排出3×12=36个四位数,
同理,若重复的数字为2,也可以排出36个重复数字;
③、若取出的4张卡片为2张1和2张2,
在4个位置安排两个1,有C42=6种情况,剩余位置安排两个2,
则可以排出6×1=6个四位数;
④、取出的4张卡片中有3个重复数字,则重复的数字为1,
在2、3、4中取出1个卡片,有C31=3种取法,安排在四个位置中,有C41=4种情况,剩余位置安排1,
可以排出3×4=12个四位数;
则一共有24+36+36+6+12=114个四位数;
故选C.
点评 本题考查排列组合的运用,解题时注意其中重复的数字,要结合题意,进行分类讨论.

练习册系列答案
相关题目
16.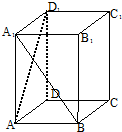 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
13.以直角坐标系的原点为极点x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.则曲线C1:ρ2-2ρcosθ-1=0上的点到曲线C2:$\left\{\begin{array}{l}{x=3-t}\\{y=1+t}\end{array}\right.$(t为参数)上的点的最短距离为( )
| A. | $2\sqrt{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
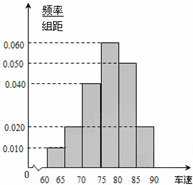 2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.
2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.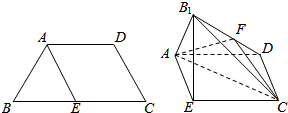 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.