题目内容
13.已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项.(1)求数列{an}的通项公式;
(2)若bn=an+(-1)nlog2an,其前n项和为Tn,求T2n-1.
分析 (1)根据条件,建立方程组即可求出数列{an}的通项公式;
(2)利用分组求和方法,对n讨论是奇数和偶数,即可得到T2n-1.
解答 解:(1)设单调递增的等比数列{an}的公比为q,
∵a3+2是a2,a4的等差中项,
∴2(a3+2)=a2+a4,
即 a1q+a1q3-2a1q2=4,
又a2+a3+a4=28,
即a1q+a1q2+a1q3=28,
∴q=$\frac{1}{2}$(舍去)或q=2,
∴a1=2,
∴an=2n.
(2)由(1)知an=2n.
∴bn=an+(-1)nlog2an=2n+(-1)n•n,
当n为奇数时,前n项和为Tn=(2+4+…+2n)+(-1+2-3+4+…-n)
=$\frac{2(1-{2}^{n})}{1-2}$+$\frac{n-1}{2}$-n,
当n为偶数时,前n项和为Tn=(2+4+…+2n)+(-1+2-3+4+…+n)
=$\frac{2(1-{2}^{n})}{1-2}$+$\frac{n}{2}$,
即有T2n-1=$\frac{2(1-{2}^{2n-1})}{1-2}$+$\frac{2n-1-1}{2}$-(2n-1)
=22n-n.
点评 本题主要考查数列的通项公式和前n项和的计算,要求熟练掌握分组求和的方法进行求和,考查学生的计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.函数y=log${\;}_{\frac{1}{2}}$(sin2xcos$\frac{π}{4}$-cos2xsin$\frac{π}{4}$)的单调递减区间是( )
| A. | (kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$),k∈Z | B. | (kπ+$\frac{π}{8}$,kπ+$\frac{3π}{8}$),k∈Z | ||
| C. | (kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$),k∈Z | D. | (kπ+$\frac{3π}{8}$,kπ+$\frac{5π}{8}$),k∈Z |
2.大量统计数据表明,某班一周内(周一到周五)各天语文、数学、外语三科有作业的概率如下表:
根据上表:
(Ⅰ)求周五没有语文、数学、外语三科作业的概率;
(Ⅱ)设一周内有数学作业的天数为ξ,求随机变量ξ的分布列和数学期望.
| 周一 | 周二 | 周三 | 周四 | 周五 | |
| 语文 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 数学 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 外语 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
(Ⅰ)求周五没有语文、数学、外语三科作业的概率;
(Ⅱ)设一周内有数学作业的天数为ξ,求随机变量ξ的分布列和数学期望.
3.设x,y满足不等式组$\left\{{\begin{array}{l}{x+y-6≤0}\\{2x-y-1≤0}\\{3x-y-2≥0}\end{array}}\right.$,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
| A. | [-1,2] | B. | [-2,1] | C. | [-3,-2] | D. | [-3,1] |
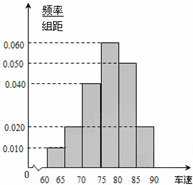 2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.
2014年“五一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图所示的频率分布直方图.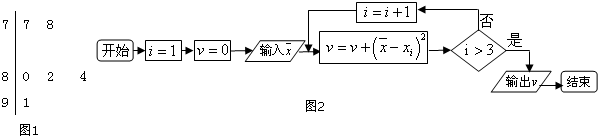 .
.