题目内容
10.${∫}_{0}^{1}$($\sqrt{1-{x}^{2}}$-x)dx=-$\frac{1}{4}$.分析 ${∫}_{0}^{1}$($\sqrt{1-{x}^{2}}$)dx利用其几何意义求值,${∫}_{0}^{1}$(-x)dx利用微积分基本道理求值.
解答 解:原式=${∫}_{0}^{1}\sqrt{1-{x}^{2}}dx-{∫}_{0}^{1}xdx$=$\frac{1}{4}-\frac{1}{2}{x}^{2}{|}_{0}^{1}$=$\frac{1}{4}-\frac{1}{2}=-\frac{1}{4}$;
故答案为:-$\frac{1}{4}$.
点评 本题考查了定积分的计算;前半部分用到定积分的几何意义求值,后半部分是求出被积函数的原函数求值.

练习册系列答案
相关题目
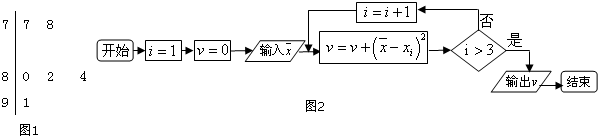
2.大量统计数据表明,某班一周内(周一到周五)各天语文、数学、外语三科有作业的概率如下表:
根据上表:
(Ⅰ)求周五没有语文、数学、外语三科作业的概率;
(Ⅱ)设一周内有数学作业的天数为ξ,求随机变量ξ的分布列和数学期望.
| 周一 | 周二 | 周三 | 周四 | 周五 | |
| 语文 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 数学 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 外语 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
(Ⅰ)求周五没有语文、数学、外语三科作业的概率;
(Ⅱ)设一周内有数学作业的天数为ξ,求随机变量ξ的分布列和数学期望.
19.某几何体的三视图如图所示(其中侧视图中的圆弧是半圆),则该几何体的表面积为( ) 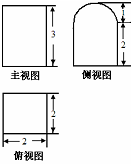

| A. | 20+2π | B. | 20+3π | C. | 24+3π | D. | 24+3π |
20.执行如图所示的程序框图,若输出S=15,则框图中①处可以填入 ( )
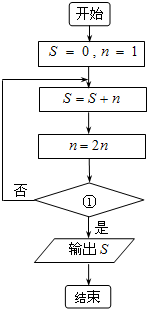

| A. | n≥4? | B. | n≥8? | C. | n≥16? | D. | n<16? |
 .
.