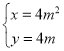题目内容
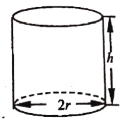
【题目】某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计),易拉罐的体积为![]() ,设圆柱的高度为
,设圆柱的高度为![]() ,底面半径为
,底面半径为![]() ,且
,且![]() ,假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为
,假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为![]() 元
元![]() ,易拉罐上下底面的制造费用均为
,易拉罐上下底面的制造费用均为![]() 元
元![]() 为常数).
为常数).
(1)写出易拉罐的制造费用![]() (元)关于
(元)关于![]() 的函数表达式,并求其定义域;
的函数表达式,并求其定义域;
(2)求易拉罐制造费用最低时![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)当
;(2)当![]() 时,
时, ![]() ,易拉罐的制造费用最低,当
,易拉罐的制造费用最低,当![]() 时,
时,![]() ,易拉罐的制造费用最低.
,易拉罐的制造费用最低.
【解析】
(1)根据体积的值,得出![]() 与
与![]() 的关系,然后将表面积公式中的
的关系,然后将表面积公式中的![]() 转化为
转化为![]() ,再根据
,再根据![]() 等条件得出定义域;
等条件得出定义域;
(2)利用导数求出函数的单调性,进而求出最值.
解:(1)因为体积为![]()
故![]() ,即
,即![]() ,
,
易拉罐的侧面积为![]() ,
,
易拉罐的上下两底面的面积为![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以有![]() ,解得
,解得![]() ,
,
故![]() ,
,
易拉罐的制造费用为![]() ;
;
(2)![]() ,
,
令![]() ,解得
,解得![]() ,
,
![]() 若
若![]() ,即
,即![]() ,此时
,此时![]()
当![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() ,函数
,函数![]() 单调递增,
单调递增,
故当![]() ,此时函数
,此时函数![]() 取得最小值,即易拉罐的制造费用最低;
取得最小值,即易拉罐的制造费用最低;
![]() 若
若![]() ,即
,即![]() ,此时
,此时![]() ,
,
当![]() 时,函数
时,函数![]() 单调递减,
单调递减,
故当![]() ,此时函数
,此时函数![]() 取得最小值,即易拉罐的制造费用最低;
取得最小值,即易拉罐的制造费用最低;
综上:当![]() 时,
时, ![]() ,易拉罐的制造费用最低,
,易拉罐的制造费用最低,
当![]() 时,
时,![]() ,易拉罐的制造费用最低.
,易拉罐的制造费用最低.

【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研究投入.为了对新研发的产品进行合理定价,将该产品按事先拟定的价格试销,得到一组检测数据如表所示:
试销价格 |
|
|
|
|
|
|
产品销量 |
|
|
|
|
|
|
已知变量![]() ,
,![]() 具有线性相关关系,现有甲、乙、丙三位同学通过计算求得回归直线方程分别为:甲/span>
具有线性相关关系,现有甲、乙、丙三位同学通过计算求得回归直线方程分别为:甲/span>![]() ;乙
;乙![]() ;丙
;丙![]() ,其中有且仅有一位同学的计算结果是正确的.
,其中有且仅有一位同学的计算结果是正确的.
(1)试判断谁的计算结果正确?求回归方程。
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”.现从检测数据中随机抽取3个,求“理想数据”的个数![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】为了研究学生的数学核心素养与抽象能力(指标![]() )、推理能力(指标
)、推理能力(指标![]() )、建模能力(指标
)、建模能力(指标![]() )的相关性,将它们各自量化为1、2、3三个等级,再用综合指标
)的相关性,将它们各自量化为1、2、3三个等级,再用综合指标![]() 的值评定学生的数学核心素养,若
的值评定学生的数学核心素养,若![]() ,则数学核心素养为一级;若
,则数学核心素养为一级;若![]() ,则数学核心素养为二级;若
,则数学核心素养为二级;若![]() ,则数学核心素养为三级,为了了解某校学生的数学核心素养,调查人员随机访问了某校10名学生,得到如下数据:
,则数学核心素养为三级,为了了解某校学生的数学核心素养,调查人员随机访问了某校10名学生,得到如下数据:
学生编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在这10名学生中任取两人,求这两人的建模能力指标相同条件下综合指标值也相同的概率;
(2)在这10名学生中任取三人,其中数学核心素养等级是一级的学生人数记为![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望.
的分布列及其数学期望.