题目内容
【题目】在平面直角坐标系xOy中,已知曲线C1:![]() (t为参数),C2:
(t为参数),C2: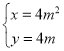 (m为参数).
(m为参数).
(1)将C1,C2的方程化为普通方程,并说明它们分别表示什么曲线;
(2)设曲线C1与C2的交点分别为A,B,O为坐标原点,求△OAB的面积的最小值.
【答案】(1)![]() sinθx-cosθy﹣2sin θ=0,
sinθx-cosθy﹣2sin θ=0,![]() y2=4x,(2)4
y2=4x,(2)4![]() .
.
【解析】
(1)C1:将![]() 两边同时乘以
两边同时乘以![]() 将
将![]() 两边同时乘以
两边同时乘以![]() ,消去参数t即可,C2消去m即可;
,消去参数t即可,C2消去m即可;
(2)联立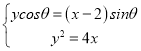 得y2sinθ﹣4ycosθ﹣8sinθ=0,设A(x1,y1),B(x2,y2),则y1+y2
得y2sinθ﹣4ycosθ﹣8sinθ=0,设A(x1,y1),B(x2,y2),则y1+y2![]() ,y1y2=﹣8,代入S△OAB=
,y1y2=﹣8,代入S△OAB=![]() |y1﹣y2|计算即可.
|y1﹣y2|计算即可.
(1)由C1:![]() (t为参数)消去t得C1:cosθy=sinθ(x﹣2),得sinθx-cosθy-2sinθ=0,
(t为参数)消去t得C1:cosθy=sinθ(x﹣2),得sinθx-cosθy-2sinθ=0,
由C2: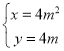 (m为参数)消去m得C2:y2=4x,
(m为参数)消去m得C2:y2=4x,
(2)联立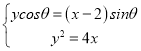 消去x得y2sinθ﹣4ycosθ﹣8sinθ=0,
消去x得y2sinθ﹣4ycosθ﹣8sinθ=0,
设A(x1,y1),B(x2,y2),则y1+y2![]() ,y1y2=﹣8,又C1与x轴的交点(2,0)
,y1y2=﹣8,又C1与x轴的交点(2,0)
∴S△OAB=![]() |y1﹣y2|
|y1﹣y2|![]()
![]()
=![]() ,
,
所以 sinθ=1时,SOAB取得最小值4![]() .
.

练习册系列答案
相关题目