题目内容
【题目】已知数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列,数列
的等差数列,数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列.
的等比数列.
(1)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和;
项和;
(2)若存在正整数![]() ,使得
,使得![]() ,试比较
,试比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
【答案】(1)![]() ;(2) 当
;(2) 当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
审题引导:①等差数列与等比数列对应项的积错位相减求和;②作差比较.
规范解答:解:(1)依题意,a5=b5=b1q5-1=1×34=81,故d=![]() =20,
=20,
所以an=1+20(n-1)=20n-19.(3分)
令Sn=1×1+21×3+41×32+…+(20n-19)·3n-1,①
则3Sn=1×3+21×32+…+(20n-39)·3n-1+(20n-19)·3n,②
①-②,得-2Sn=1+20×(3+32+…+3n-1)-(20n-19)·3n=1+20×![]() -(20n-19)·3n=(29-20n)·3n-29,所以Sn=
-(20n-19)·3n=(29-20n)·3n-29,所以Sn=![]() .(7分)
.(7分)
(2)因为ak=bk,所以1+(k-1)d=qk-1,即d=![]() ,
,
故an=1+(n-1)![]() .又bn=qn-1,(9分)所以bn-an=qn-1-
.又bn=qn-1,(9分)所以bn-an=qn-1-![]()
=![]() [(k-1)(qn-1-1)-(n-1)(qk-1-1)]
[(k-1)(qn-1-1)-(n-1)(qk-1-1)]
=![]() [(k-1)(qn-2+qn-3+…+q+1)-(n-1)(qk-2+qk-3+…+q+1)].(11分)
[(k-1)(qn-2+qn-3+…+q+1)-(n-1)(qk-2+qk-3+…+q+1)].(11分)
(ⅰ)当1<n<k时,由q>1知
bn-an=![]() [(k-n)(qn-2+qn-3+…+q+1)-(n-1)(qk-2+qk-3+…+qn-1)]
[(k-n)(qn-2+qn-3+…+q+1)-(n-1)(qk-2+qk-3+…+qn-1)]
<![]() [(k-n)(n-1)qn-2-(n-1)(k-n)qn-1]=-
[(k-n)(n-1)qn-2-(n-1)(k-n)qn-1]=-![]()
<0;(13分)
(ⅱ)当n>k时,由q>1知
bn-an=![]() [(k-1)(qn-2+qn-3+…+qk-1)-(n-k)(qk-2+qk-3+…+q+1)]
[(k-1)(qn-2+qn-3+…+qk-1)-(n-k)(qk-2+qk-3+…+q+1)]
>![]() [(k-1)(n-k)qk-1-(n-k)(k-1)qk-2]
[(k-1)(n-k)qk-1-(n-k)(k-1)qk-2]
=(q-1)2qk-2(n-k)
>0,(15分)
综上所述,当1<n<k时,an<bn;当n>k时,an>bn;当n=1,k时,an=bn.(16分)
(注:仅给出“1<n<k时,an<bn;n>k时,an>bn”得2分)
错因错位相减时项数容易搞错,作差比较后学生不能灵活倒用等比数列求和公式1-qn=(1-q)(1+q+q2+…+qn-1)

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】随着互联网经济不断发展,网上开店销售农产品的人群越来越多,网上交易额也逐年增加,某一农户农产品连续五年的网银交易额统计表,如下所示:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
网上交易额 | 5 | 6 | 7 | 8 | 10 |
经研究发现,年份与网银交易额之间呈线性相关关系,为了计算的方便,农户将上表的数据进行了处理,![]() ,得到如表:
,得到如表:
时间代号 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)通过(1)中的方程.求出![]() 关于
关于![]() 的回归方程;并用所求回归方程预测到2020年年底,该农户网店网银交易额可达多少?
的回归方程;并用所求回归方程预测到2020年年底,该农户网店网银交易额可达多少?
(附:在线性回归方程![]() 中,
中,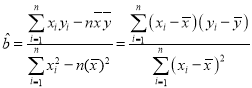 ,
,![]() )
)