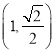题目内容
【题目】一元线性同余方程组问题最早可见于中国南北朝时期(公元![]() 世纪)的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”问题,原文如下:有物不知数,三三数之剩二,五五数之剩三,问物几何?即,一个整数除以三余二,除以五余三,求这个整数.设这个整数为
世纪)的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”问题,原文如下:有物不知数,三三数之剩二,五五数之剩三,问物几何?即,一个整数除以三余二,除以五余三,求这个整数.设这个整数为![]() ,当
,当![]() 时, 符合条件的
时, 符合条件的![]() 共有_____个.
共有_____个.
【答案】![]()
【解析】
由题设a=3m+2=5n+3,m,n∈N*,得3m=5n+1,对m讨论求解即可
由题设a=3m+2=5n+3,m,n∈N*,则3m=5n+1
当m=5k,n不存在;
当m=5k+1,n不存在
当m=5k+2,n=3k+1,满足题意
当m=5k+3,n不存在;
当m=5k+4,n不存在;
故2≤a=15k+8≤2019,解![]() 则k=0,1,2…134,共135个
则k=0,1,2…134,共135个
故答案为:135

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
【题目】某果农从经过筛选(每个水果的大小最小不低于50克,最大不超过100克)的10000个水果中抽取出100个样本进行统计,得到如下频率分布表:
级别 | 大小(克) | 频数 | 频率 |
一级果 |
| 5 | 0.05 |
二级果 |
|
| |
三级果 |
| 35 |
|
四级果 |
| 30 | |
五级果 |
| 20 | |
合计 | 100 |
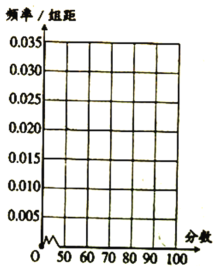
请根据频率分布表中所提供的数据,解得下列问题:
(1)求![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(2)若从四级果,五级果中按分层抽样的方法抽取5个水果,并从中选出2个作为展品,求2个展品中仅有1个是四级果的概率;
(3)若将水果作分级销售,预计销售的价格![]() 元/个与每个水果的大小
元/个与每个水果的大小![]() 克关系是:
克关系是: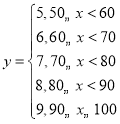 ,则预计10000个水果可收入多少元?
,则预计10000个水果可收入多少元?