题目内容
13.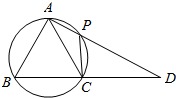 如图所示,在四边形ABCP中,线段AP与BC的延长线交于点D,已知AB=AC且A,B,C,P四点共圆.
如图所示,在四边形ABCP中,线段AP与BC的延长线交于点D,已知AB=AC且A,B,C,P四点共圆.(1)求证:AC•DP=BD•PC
(2)若△ABC是面积为4$\sqrt{3}$的等边三角形,求AP•AD的值.
分析 (1)证明△DPC∽△DBA,所以$\frac{PC}{AB}$=$\frac{PD}{BD}$,利用AB=AC,可得结论;
(2)求出AC=4,证明△APC∽△ACD,所以$\frac{AP}{AC}$=$\frac{AC}{AD}$,所以AP•AD=AC2=16.
解答 (1)证明:因为点A,B,C,P四点共圆,所以∠ABC+∠APC=180°,
因为∠DPC+∠APC=180°,所以∠DPC=∠ABC,
因为∠D=∠D,所以△DPC∽△DBA,所以$\frac{PC}{AB}$=$\frac{PD}{BD}$,
因为AB=AC,所以$\frac{PC}{AC}$=$\frac{PD}{BD}$.即AC•DP=BD•PC …(5分)
(2)解:因为△ABC是面积为4$\sqrt{3}$的等边三角形,
所以AB=AC=4,
因为AB=AC,所以∠ACB=∠ABC,
又∠ACD+∠ACB=180°,所以∠ACD+∠ABC=180°.
由于∠ABC+∠APC=180°,所以∠ACD=∠APC,
又∠CAP=∠DAC,所以△APC∽△ACD,所以$\frac{AP}{AC}$=$\frac{AC}{AD}$,所以AP•AD=AC2=16.…(10分)
点评 本题考查的知识点:四点共圆的性质,三角形相似的判定和性质.属于中档题.

练习册系列答案
相关题目
3.平行四边形ABCD中,AC与BD交于点O,M为OC的中点,若$\overrightarrow{AB}$=(2,4),$\overrightarrow{AC}$=(1,3),则$\overrightarrow{AD}•\overrightarrow{BM}$等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 3 | D. | -3 |
 如图边长为2的正方形内部有一块不规则的区域E,若向该图中随机撒100颗豆子,经清点落在E内的有30颗,试估计E的面积为:1.2.
如图边长为2的正方形内部有一块不规则的区域E,若向该图中随机撒100颗豆子,经清点落在E内的有30颗,试估计E的面积为:1.2.