题目内容
9．cos23°sin53°-sin23°cos53°=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | 1 |
分析 根据两角差的正弦公式，计算即可，sin（α-β）=sinαcosβ-cosαsinβ．
解答 解：cos23°sin53°-sin23°cos53°=sin（53°-23°）=sin30°=$\frac{1}{2}$，
故选：A．
点评 本题考查了根据两角差的正弦公式，sin（α-β）=sinαcosβ-cosαsinβ．属于基础题．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
19．定义运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，若函数f（x）=$|\begin{array}{l}{x-1}&{2}\\{-x}&{x+3}\end{array}|$在（-∞，m）上单调递减，则实数m的取值范围（ ）
| A． | （-2，+∞） | B． | [-2，+∞） | C． | （-∞，-2） | D． | （-∞，-2] |
14．
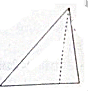已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成，其正视图为如图所示的直角三角形（其中虚线长度为$\sqrt{5}$），则此四棱锥的体积是（ ）
已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成，其正视图为如图所示的直角三角形（其中虚线长度为$\sqrt{5}$），则此四棱锥的体积是（ ）| A． | 14 | B． | 7$\sqrt{5}$ | C． | $\frac{14}{3}$ | D． | $\frac{2\sqrt{5}}{3}$ |