题目内容
20．△ABC中，a、b、c分别为∠A、∠B、∠C的对边，如果a、b、c成等差数列，∠B=30°，△ABC的面积为2-$\sqrt{3}$，那么b=$\frac{2\sqrt{3}}{3}$．分析 根据等差中项的性质可知2b=a+c．平方后整理得a2+c2=4b2-2ac．利用三角形面积求得ac的值，进而把a2+c2=4b2-2ac．代入余弦定理求得b的值．
解答 解：∵a，b，c成等差数列，
∴2b=a+c．
平方得a2+c2=4b2-2ac．
又△ABC的面积为2-$\sqrt{3}$，且∠B=30°，
故由S△=$\frac{1}{2}$acsinB=$\frac{1}{2}$ac•sin30°=$\frac{1}{4}$ac=2-$\sqrt{3}$，
得ac=8-4$\sqrt{3}$，
∴a2+c2=4b2-16+8$\sqrt{3}$．
由余弦定理
cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{3{b}^{2}-16+8\sqrt{3}}{16-8\sqrt{3}}$=$\frac{\sqrt{3}}{2}$．
解得b=$\frac{2\sqrt{3}}{3}$．
故答案为：$\frac{2\sqrt{3}}{3}$．
点评 本题主要考查了解三角形的问题．解题过程中常需要正弦定理，余弦定理，三角形面积公式以及勾股定理等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
10．双曲线两条渐近线的夹角为60°，该双曲线的离心率为（ ）
| A． | $\frac{2}{3}\sqrt{3}$或2 | B． | $\frac{2}{3}\sqrt{3}$或$\sqrt{2}$ | C． | $\sqrt{3}$或2 | D． | $\sqrt{3}$或$\sqrt{2}$ |
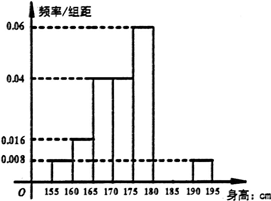某学校进行体检，现得到所有男生的身高数据，从中随机抽取50人进行统计（已知这50人身材介于155cm到195cm之间），现将抽取结果按如下方式分成八组：第一组[155，160），第二组[160，165），…，第八组[190，195]，并按此分组绘制如下图所示的频率分布直方图，其中，第六组和第七组还没有绘制完成，已知第一组与第八组人数相同，第七组的人数为3人．
9．cos23°sin53°-sin23°cos53°=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | 1 |
在四棱锥P-ABCD中，底面ABCD为边长为a的菱形，∠BAD=60°，△PAD为正三角形，平面PAD⊥平面ABCD，E、H分别为BC、AD的中点，F在PC边上，且PF=2FC．