题目内容
14.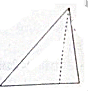 已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),则此四棱锥的体积是( )
已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),则此四棱锥的体积是( )| A. | 14 | B. | 7$\sqrt{5}$ | C. | $\frac{14}{3}$ | D. | $\frac{2\sqrt{5}}{3}$ |
分析 确定四棱锥的底面面积,利用锥体的体积公式,求出四棱锥的体积.
解答 解:由题意,四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其面积为$\frac{1}{2}×4×4$-$\frac{1}{2}×2×1$=7,
∵正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),
∴此四棱锥的体积是$\frac{1}{3}×7×\sqrt{5}$=$\frac{7\sqrt{5}}{3}$,
故选:D.
点评 本题考查四棱锥的体积,考查线性规划知识,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
9.cos23°sin53°-sin23°cos53°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
3.设集合P={x|y=log2x},Q=|y|y=x3},则P∩Q等于( )
| A. | R | B. | [0,+∞) | C. | (0,+∞) | D. | [1,+∞) |