题目内容
18.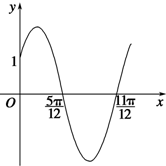 已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x-$\frac{π}{12}$)-f(x+$\frac{π}{12}$)的单调递增区间.
分析 (1)根据三角函数图象确定A,ω和φ的值即可求函数f(x)的解析式;
(2)化简g(x),然后根据三角函数的单调性进行求解即可
解答 解:(1)由图可知$\frac{T}{2}=\frac{11π}{12}-\frac{5π}{12}$,可得T=π,
则$\frac{2π}{ω}=π$,则ω=2,
又图象经过($\frac{5π}{12}$,0),
故有2×$\frac{5π}{12}$+φ=kπ,k∈Z,得φ=-$\frac{5π}{6}$+kπ,
又0<φ<$\frac{π}{2}$,取φ=$\frac{π}{6}$.
过(0,1)点,
所以Asinφ=1,可得A=2.
得f(x)=2sin(2x+$\frac{π}{6}$).
(2)g(x)=f(x-$\frac{π}{12}$)-f(x+$\frac{π}{12}$)=2sin[2(x-$\frac{π}{12}$)+$\frac{π}{6}$]-2sin[2(x+$\frac{π}{12}$)+$\frac{π}{6}$]
=2sin2x-2sin(2x+$\frac{π}{3}$)=2sin2x-2sin2xcos$\frac{π}{3}$-2cos2xsin$\frac{π}{3}$=sin2x-$\sqrt{3}$cos2x
=2sin(2x-$\frac{π}{3}$),
由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,
得kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$,k∈Z,
所以g(x)的单调递增区间为[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$],k∈Z.
点评 本题主要考查三角函数的解析式的求解以及三角函数单调区间的求解,根据图象确定函数的解析式是解决本题的关键.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案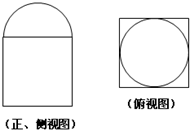 如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )
如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )| A. | 8+$\frac{2}{3}$π | B. | 8+$\frac{4}{3}$π | C. | 24+π | D. | 20+2π |
| A. | $\frac{3\sqrt{5}}{10}$ | B. | $\frac{6\sqrt{5}}{5}$ | C. | $\frac{3\sqrt{5}}{20}$ | D. | $\frac{7\sqrt{5}}{10}$ |