题目内容
3.一个正四面体木块的四个面上分别写有数字1,2,3,4,将三个这样的四面体木块抛于桌面上,记与桌面贴合的一面上的数字分别为x,y,z.(1)求x+y+z=6的概率;
(2)求xyz能被3整除的概率.
分析 试验的基本事件结果为43=64个,
(1)事件D=“x+y+z=6”,由题知,它可以分解为三个互斥事件,A=“x=y=z=2“,B=“x,y,z分别取1,2,3”,C=“x,y,z两个取1一个取4”,根据互斥事件的加法公式,计算即可;
(2)设事件E=“xyz能被3整除”,则E的对立事件是$\overline{E}$=“x,y,z中没有数字3”,根据互斥对立事件的概率公式计算即可.
解答 解:试验的基本事件结果为43=64个,
(1)设事件D=“x+y+z=6”,由题知,它可以分解为三个互斥事件,A=“x=y=z=2“,B=“x,y,z分别取1,2,3”,C=“x,y,z两个取1一个取4”,
所以P(A)=$\frac{1}{64}$,P(B)=$\frac{{A}_{3}^{3}}{64}$=$\frac{6}{64}$,P(C)=$\frac{{C}_{3}^{1}}{64}$=$\frac{3}{64}$,
所以P(D)=P(A)+P(B)+P(C)=$\frac{10}{64}$=$\frac{5}{32}$;
(2)设事件E=“xyz能被3整除”,则E的对立事件是$\overline{E}$=“x,y,z中没有数字3”,
故P(E)=1-P($\overline{E}$)=1-$\frac{{3}^{3}}{64}$=$\frac{37}{64}$.
点评 本题考查了等可能事件的概率公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
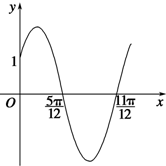 已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.