题目内容
6.在△ABC中,(1)求证:a:b:c=sinA:sinB:sinC
(2)若a:b:c=3:5:7,求sinA+sinB+sinC.
分析 (1)作AD⊥BC于D,由AD=csinB=bsinC,可得b:c=sinB:sinC,同理可得:a:b=sinA:sinB,即可得证.
(2)设a=3x,则b=5x,c=7x,由余弦定理得cosC=$\frac{1}{2}$,可得$sinC=\frac{{\sqrt{3}}}{2}$,由正弦定理可得sinA+sinB+sinC=$(\frac{3}{7}+\frac{5}{7}+1)sinC=\frac{{15\sqrt{3}}}{14}$.
解答 解:(1)证明:如图作AD⊥BC于D,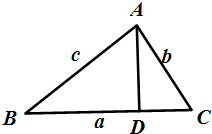
则AD=csinB=bsinC,
∴b:c=sinB:sinC,
同理:a:b=sinA:sinB,
∴a:b:c=sinA:sinB:sinC.
(2)解:设a=3x,则b=5x,c=7x,
由余弦定理得 $cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=\frac{{-15{x^2}}}{{30{x^2}}}=-\frac{1}{2}$,
∴$sinC=\frac{{\sqrt{3}}}{2}$,
∴sinA+sinB+sinC=$(\frac{3}{7}+\frac{5}{7}+1)sinC=\frac{{15\sqrt{3}}}{14}$.
点评 本题主要考查了正弦定理,余弦定理的综合应用,属于基本知识的考查.

练习册系列答案
相关题目
18.下列函数中既是偶函数又在(0,+∞)上是增函数的是( )
| A. | y=x3 | B. | y=|x|-3 | C. | y=x2-2x+1 | D. | y=2-|x| |
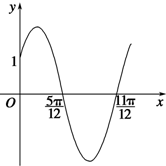 已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.