题目内容
10.二人相约12:00~13:00在体育场见面,假定每人在这段时间内的每个时刻到达该地点的可能性是相同的,先到者等20分钟就可离去,试求这两人会面的概率.分析 由题意设事件A为“甲乙两人能会面”,求出试验包含的所有事件,并且事件对应的集合表示的面积是s=1,再求出满足条件的事件,并且得到事件对应的集合表示的面积是 $\frac{5}{9}$,进而根据几何概率模型的计算公式可得答案.
解答 解:由题意知本题是一个几何概型,设事件A为“甲乙两人能会面”,
试验包含的所有事件是Ω={(x,y)|12<x<13,12<y<13},并且事件对应的集合表示的面积是s=1,
满足条件的事件是A={(x,y)|12<x<13,12<y<13,|x-y|<$\frac{20}{60}=\frac{1}{3}$}
所以事件对应的集合表示的面积是1-2×$\frac{1}{2}$×$\frac{2}{3}$×$\frac{2}{3}$=$\frac{5}{9}$,
根据几何概型概率公式得到P=$\frac{5}{9}$.
所以两人能会面的概率是$\frac{5}{9}$.
点评 本题考查了几何概型的概率求法;解决此类问题的关键是熟练掌握几何概型的定义与概率计算公式,而几何概率模型一般通过事件的长度、面积或者体积之比来求事件发生的概率,因此只要根据题意判断出题目是属于那种类型即可,此题属于中档题,是根据面积之比来计算事件发生的概率.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
18.下列函数中既是偶函数又在(0,+∞)上是增函数的是( )
| A. | y=x3 | B. | y=|x|-3 | C. | y=x2-2x+1 | D. | y=2-|x| |
19.在等腰直角三角形ABC中,角C为直角.在∠ACB内部任意作一条射线CM,与线段AB交于点M,则AM<AC的概率( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
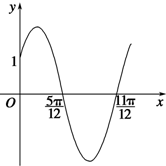 已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.