题目内容
7.已知数列{an}满足a1=1,a2=a>0,数列{bn}满足bn=an•an+1(1)若{an}为等比数列,求{bn}的前n项的和sn;
(2)若${b_n}={3^n}$,求数列{an}的通项公式;
(3)若bn=n+2,求证:$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{a_n}>2\sqrt{n+2}-3$.
分析 (1)${a_n}={a^{n-1}}$,可得${b_n}={a^{n-1}}•{a^n}={a^{2n-1}}$.对a分类讨论,利用等比数列的前n项和公式即可得出.
(2)由3n=an•an+1,3n-1=an-1•an(n≥2,n∈N),可得$\frac{{{a_{n+1}}}}{{{a_{n-1}}}}=3(n≥2,n∈N)$,对n分类讨论利用等比数列的通项公式即可得出.
(3)由anan+1=n+2,an-1an=n+1(n≥2),可得an+1-an-1=$\frac{1}{{a}_{n}}$(n≥2).于是$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+$…+$\frac{1}{{a}_{n}}$=an+1+an-a1-a2+$\frac{1}{{a}_{1}}$,再利用基本不等式的性质即可得出.
解答 (1)解:∵${a_n}={a^{n-1}}$,
∴${b_n}={a^{n-1}}•{a^n}={a^{2n-1}}$.
当a=1时,bn=1,则sn=n.
当a≠1时,${s_n}=\frac{{a(1-{a^{2n}})}}{{1-{a^2}}}$.
(2)解:∵3n=an•an+1,
∴3n-1=an-1•an(n≥2,n∈N),
∴$\frac{{{a_{n+1}}}}{{{a_{n-1}}}}=3(n≥2,n∈N)$,
当n=2k+1,(k∈N*)时,∴$\frac{{a}_{2k+2}}{{a}_{2k}}$=3(k∈N*),
∴a2k=a2•3k-1=a•3k-1.
当n=2k,(k∈N*)时,
∴$\frac{{a}_{2k+1}}{{a}_{2k-1}}$=3(k∈N*),
∴a2k-1=3k-1.
∴${a_n}=\left\{\begin{array}{l}{3^{\frac{n-1}{2}}}(n=2k-1)\\ a{3^{\frac{n-2}{2}}}(n=2k)\end{array}\right.$.
(3)证明:∵anan+1=n+2,①
∴an-1an=n+1(n≥2),②
①-②得an(an+1-an-1)=1,∴an+1-an-1=$\frac{1}{{a}_{n}}$(n≥2).
∴$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+$…+$\frac{1}{{a}_{n}}$
=(a3-a1)+(a4-a2)+…+(an+1-an-1)
=an+1+an-a1-a2+$\frac{1}{{a}_{1}}$
=an+an+1-3$≥2\sqrt{{a}_{n}•{a}_{n+1}}$-3=2$\sqrt{n+2}$-3.
∴$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{a_n}>2\sqrt{n+2}-3$.
点评 本题考查了递推式的应用、等比数列的通项公式及其前n项和公式、分类讨论方法、基本不等式的性质,考查了推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | y=x3 | B. | y=|x|-3 | C. | y=x2-2x+1 | D. | y=2-|x| |
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
| A. | 1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…<$\frac{1}{2n-1}$ | B. | 1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…$\frac{1}{{n}^{2}}$<$\frac{1}{2n-1}$ | ||
| C. | 1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…$\frac{1}{{n}^{2}}$<$\frac{2n-1}{n}$ | D. | 1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…$\frac{1}{{n}^{2}}$<$\frac{2n}{2n+1}$ |
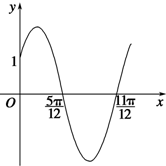 已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.