题目内容
10.若动点A,B分别在直线l1:x+2y-1=0和l2:2x+4y+5=0上移动,则|$\overrightarrow{OA}$+$\overrightarrow{OB}$|(O为原点)的最小值是( )| A. | $\frac{3\sqrt{5}}{10}$ | B. | $\frac{6\sqrt{5}}{5}$ | C. | $\frac{3\sqrt{5}}{20}$ | D. | $\frac{7\sqrt{5}}{10}$ |
分析 根据题意,画出图形,结合图形,利用向量的几何意义,求出|$\overrightarrow{OA}$+$\overrightarrow{OB}$|的最小值.
解答 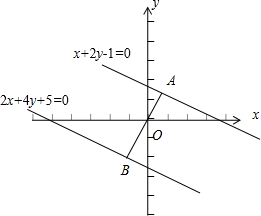 解:∵直线l1:x+2y-1=0和l2:2x+4y+5=0,
解:∵直线l1:x+2y-1=0和l2:2x+4y+5=0,
∴直线l1∥l2,
又A、B分别是直线l1与l2上的动点,
∴原点O到直线的距离是d1=$\frac{|-1|}{\sqrt{{1}^{2}{+2}^{2}}}$=$\frac{\sqrt{5}}{5}$,
O到直线的距离是d2=$\frac{|5|}{\sqrt{{2}^{2}{+4}^{2}}}$=$\frac{\sqrt{5}}{2}$;
∴|$\overrightarrow{OA}$+$\overrightarrow{OB}$|的最小值是|d1-d2|=$\frac{\sqrt{5}}{2}$-$\frac{\sqrt{5}}{5}$=$\frac{3\sqrt{5}}{10}$,
如图所示.
故选:A.
点评 本题考查了平面向量的应用问题,也考查了直线方程的应用问题,考查了数形结合的解题思想,是基础题目.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
19.在等腰直角三角形ABC中,角C为直角.在∠ACB内部任意作一条射线CM,与线段AB交于点M,则AM<AC的概率( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
20.若关于x的不等式|2x-1|≥|1+a|-|2-a|对任意实数a恒成立,则x的取值范围是( )
| A. | (-∞,0]∪[1,+∞) | B. | [0,1] | C. | (-∞,-1]∪[2,+∞) | D. | [-1,2] |
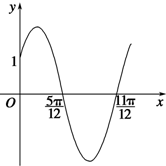 已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(wx+φ)(x∈R,w>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.