题目内容
A高校自主招生设置了先后三道程序:部分高校联合考试、本校专业考试、本校面试.在每道程序中,设置三个成绩等级:优、良、中.若考生在某道程序中获得“中”,则该考生在本道程序中不通过,且不能进入下面的程序.考生只有全部通过三道程序,自主招生考试才算通过.某中学学生甲参加A高校自主招生考试,已知该生在每道程序中通过的概率均为 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2.
(1)求学生甲不能通过A高校自主招生考试的概率;
(2)设X为学生甲在三道程序中获优的次数,求X的概率分布及数学期望.
(1) (2)X的概率分布为:
(2)X的概率分布为:X 0 1 2 3 P 




解析解:由题意,得 解得p1=p2=
解得p1=p2= .
.
(1)设事件A为学生甲不能通过A高校自主招生考试,则P(A)= +
+ ×
× +
+ ×
× ×
× =
= .
.
即学生甲不能通过A高校自主招生考试的概率为 .
.
(2)由题意知,X=0,1,2,3.
P(X=0)= +
+ ×
× +
+ ×
× ×
× +
+ ×
× ×
× =
= ,
,
P(X=2)= ×
× ×
× +
+ ×
× ×
× +
+ ×
× ×
× +
+ ×
× ×
× =
= ,P(X=3)=
,P(X=3)= ×
× ×
× =
= ,
,
∵ (X=i)=1,
(X=i)=1,
∴P(X=1)=1-P(X=0)-P(X=2)-P(X=3)= .
.
∴X的概率分布为:
X的数学期望E(X)=0×X 0 1 2 3 P 



 +1×
+1× +2×
+2× +3×
+3× =
= .
.

练习册系列答案
相关题目
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 |  | 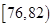 |  |  | 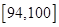 |
| 元件A | 8 | 12 | 40 | 32] | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下;
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
 ,B级考试合格的概率为
,B级考试合格的概率为 .假设各级考试成绩合格与否均互不影响.
.假设各级考试成绩合格与否均互不影响. ,求
,求 .
.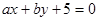 与圆
与圆 相切的概率;
相切的概率; 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率. 、
、 两个盒子中分别装有标记为
两个盒子中分别装有标记为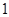 ,
, ,
, ,
, 的大小相同的四个小球,甲从
的大小相同的四个小球,甲从 表示事件“甲抽到标号为
表示事件“甲抽到标号为 的小球,乙抽到标号为
的小球,乙抽到标号为 的小球”,试写出所有可能的事件;
的小球”,试写出所有可能的事件; ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次. 的分布列和数学期望.
的分布列和数学期望.